はじめに
- これは公式ページのレッスン内容の翻訳がほとんどです
- これは公式ページのレッスンの第3部です。第1、第2をしていない方はやることをおすすめします。
- 公式ページのレッスンが途中で終わっている為、このページも途中で終わります
参照元
Lesson3 A Grid
グリッドは一般的な幾何プリミティブです。グリッドはx軸とy軸に分割された平面と考えられます。SverchokのPlaneジェネレータはグリッドを作成しますが、基本的なノードを組み合わせてゼロから作ります。これによりパラメトリック設計のいくつかの重要な概念、動的なトポロジの実用的なヒントが得られます。
Gridについて何を知っていますか?
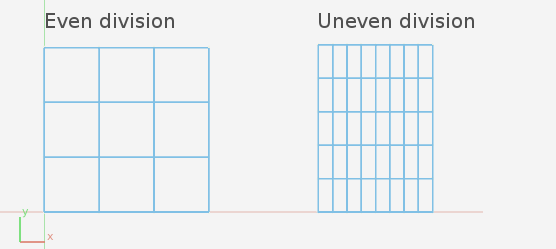
単純化のため細分化されたPlaneをテンプレートとします。私達はGridがフラットだと知っている為、3次元(z軸)は定数です。均一に細分化されたPlane、またはX軸とY軸が別々に分割されたPlaneを持つことができます。後者はより少し興味深いものです。
どこから開始すればよいか?
自明ではない主題の場合、私達はよくメモ帳を使い(紙、Blenderならグリースペンシルなどを使う)達成したいものの簡略版を書きます。図面上なら私達は簡単にプロパティを指したり名前付けができ、関係性を見たり、事前に解決する事もあります。
レッスンにGridを選択したのは数個のプロパティしか無いためです: X長、Y長、X分割数、Y分割数。これらのプロパティはいくつかの方法で表せます。2つの見方がある位置的プロパティ
公開する変数を決定する
ゼロからジェネレータを作るメリットは、自分にとって最も都合が良いものに基づいて決定を下せる事です。ここで私が最も便利だと思うものを挙げます。これは後でいつでも変更できます。
- Xの距離分割
- Yの距離分割
- Xの頂点数
- Yの頂点数
可能なら整数で考える
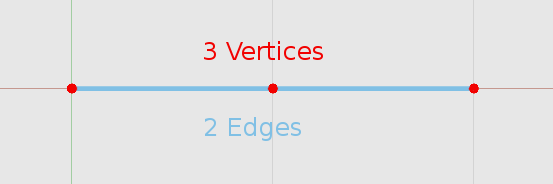
何を言いたいかというと、問題を数学的に複雑ではないものに縮小するという事です。ここに座標を図示するためにXYグラフ上に描かれたグリッドがあります。Z軸は無視できますが完全性のために含んでいます。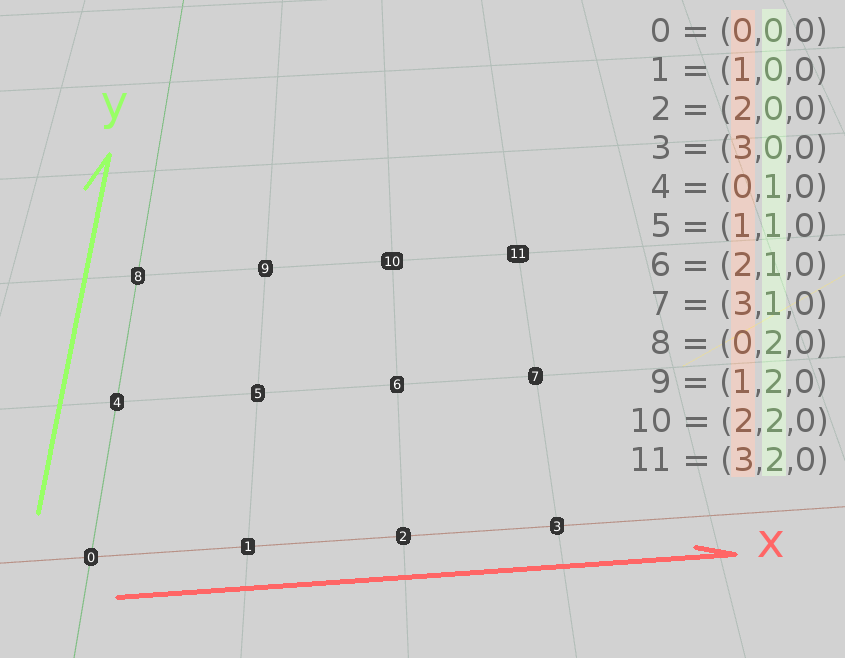
X軸が4頂点、Y軸が3頂点とした理由は、参照として使える最小で有用な頂点のセットだからです。3 * 3 や 4 * 4 としなかったのは、XYで異なった頂点数を使用する事で、X軸が4に、Y軸が3に何かしら関係がある事を明確にする為です。
各頂点の最初のインデックスを見てシーケンスを考えるなら、それは[0,1,2,3,0,1,2,3,0,1,2,3]のようになるでしょう。そのようなシーケンスは簡単に作れます。各頂点の2番目のインデックスを見るなら[0,0,0,0,1,1,1,1,2,2,2,2]となり、これも簡単に作れます。
剰余演算(modulo) と 整数除法(integer division,整数割り算) を使用してグリッド座標を取得する
Pythonを知っていたり、少なくとも %(modulo)や//(int div)を知っている事を願います。上記のシーケンスは、このようなコードで作成できます。もしコードが理解できないなら下で解説していますので読み進んでください。
# variables x = 4 y = 3 j = x * y # 12 # using for loop final_list = [] for i in range(j): x = i % 4 # makes: 0 1 2 3 0 1 2 3 0 1 2 3 y = i // 4 # makes: 0 0 0 0 1 1 1 1 2 2 2 2 z = 0 final_list.append((x, y, z)) print(final_list) ''' >> [(0, 0, 0), (1, 0, 0), (2, 0, 0), (3, 0, 0), >> (0, 1, 0), (1, 1, 0), (2, 1, 0), (3, 1, 0), >> (0, 2, 0), (1, 2, 0), (2, 2, 0), (3, 2, 0)] ''' # using list comprehension final_list = [(i%4, i//4, 0) for i in range(j)]
運が良ければ、ここのコードで迷子になって無いでしょう。視覚的プログラミングはタイピングが少ないだけで非常に似ています。ノードをクリック&ドラッグし情報のフローを生成しても、コードをテキストエディターに書いてもアルゴリズムの配管は同じです。
演算子(オペランド)
レッスン1と2ではMathノードを導入しました。このMathノードは演算子とよばれる多くのオペレーションがあります。頂点コンポーネントを取得するためにこれらに焦点を当てます。
| 演算子 | シンボル | 振る舞い |
|---|---|---|
| Modulo(mod) | % | i % 4はi / 4のあまりを返す。最も近い整数に切り捨てる |
| Integer Division | // | i // 4はi / 4の結果を返す。最も近い整数に切り捨てる。 |
i % 4は[0,1,2,3,4,5,6,7,8,9,10,11]を[0,1,2,3,0,1,2,3,0,1,2,3]に出来るi // 4は[0,1,2,3,4,5,6,7,8,9,10,11]を[0,0,0,0,1,1,1,1,2,2,2,2]に出来る
頂点の生成
Add -> Number -> A Number- X と Y の分2つ
- int
- X は4、Yは3とする
Add -> Number -> Scalar Math- 追加する Scalar Math は下記の3つ
- 配列長を計算する為の Multiply
- X の頂点を計算する Modulo
- Y の頂点を計算する Int Division
Add -> Number -> Number Range[[0,1,2,3,4,5,6,7,8,9,10,11]]の配列をリストを作成する- Int
- Stepモード
- Start 0、Step 1
Add -> Vector -> Vector In- 頂点生成用
- Viewer Index +
- 作成した頂点を可視化するためのもの
- Sthethoscope MK2 は部分部分の結果を確認するために配置
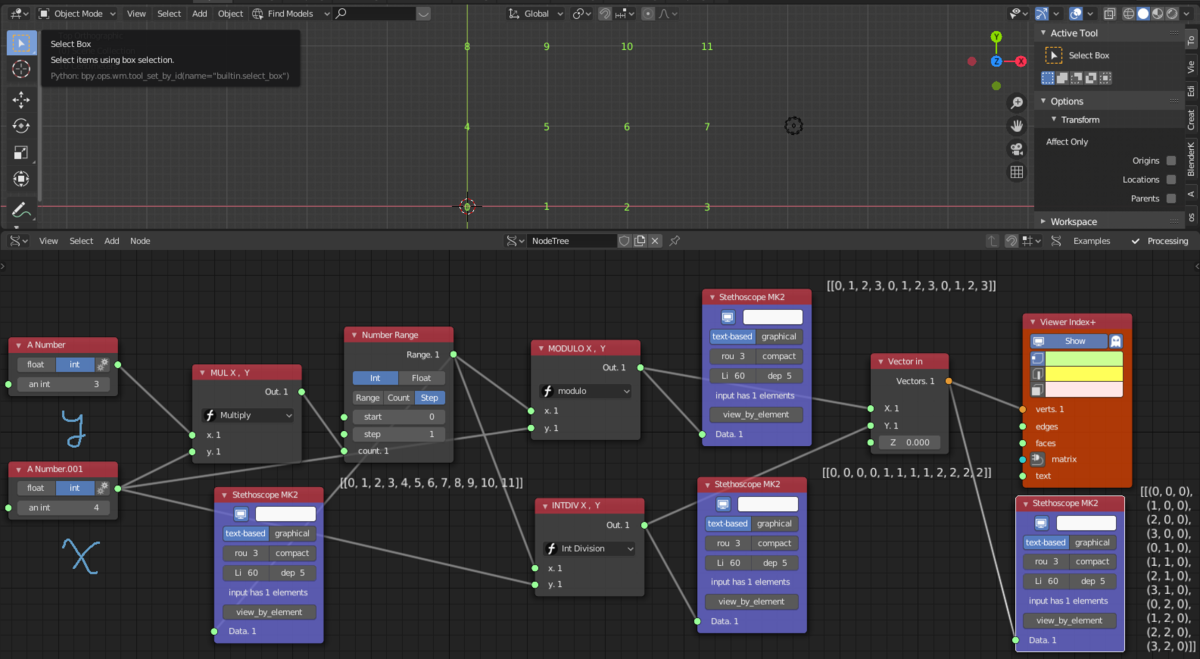
全てのノードを正しく接続すると、Vector In の出力を Viewer Index+の verts に接続した時にインデックスが表示されます。XとYの値を変更することで正しく動作しているか確認できますが、次のステップに移る前に元に戻すことを忘れないでください。
ポリゴンの生成
ある人にとっては明らかと思えるかもしれませんが、行ったことない人に向けて書きます。ここで6つのインデックスリストを書き出します(2行3ポリゴンで結果はX = 4、Y = 3グリッドとなります)。頂点を上から参照し時計回りに移動します。ポリゴンのリストに入力する順序はあなたがより都合よくなる方法を見つけることで決定します。
例えば、X軸を列と考え左から右へ、下から上へと考えればこうです。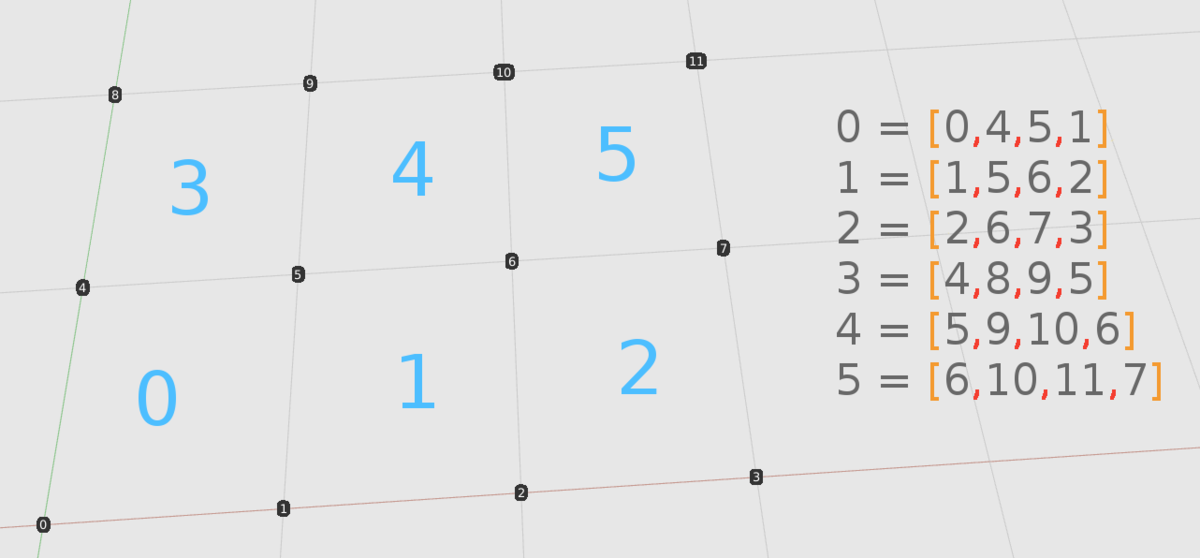
ポリゴンインデックスの2と3の間でパターンに切れ目がある事に気付いてください。頂点[3, 7, 8, 4]のポリゴンは存在しません。もし作ったら次のように次の行へ接続するようなポリゴンができます。
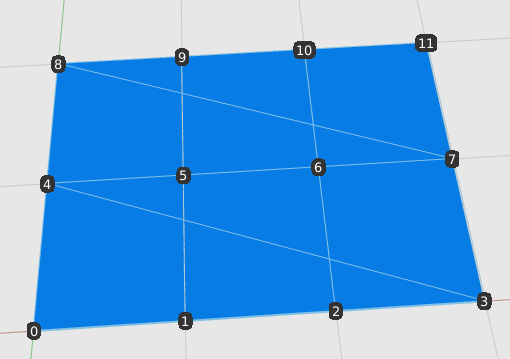
どれだけのポリゴンが必要がわかりました(この数を j とします)、0 から j - 1 または [0, 1, 2, 3, 4, 5]という範囲に基づいてインデックスシーケンスを生成するアルゴリズムを考えると便利です。n番目のポリゴンを全て削除する必要があるという事実を一旦無視するか、またはそもそも作成しないようにします。利便性と効率性の間で選択を決定する事になります。私はここでは利便性を選択します。
ポリゴンアルゴリズム
Sverchokは複雑なジオメトリを1行のコードも書かずに生成させてくれますが、熱心にコーディングを回避してもシステムを最大限に活用はできません。日常生活において曲がり角で左折をしない事を想像してみてください、目的地に到達する為のより利便性の良い方法を逃すことになります。
アルゴリズムがどのように動作するかを説明し、あなたがテスト出来るようにする為に、少しのpythonプログラムとしてアルゴリズムを示すのは私にとって簡単です。プログラミング言語は実行する事で曖昧さなしにどのように動作するかが確認できます。
作業途中 エレガントではない方法
文字とおりここで、ここのセクション途中でレッスンは終了している
これはx, y の頂点数から面を生成します。
ny = 3 nx = 4 faces = [] add_face = faces.append total_range = ((ny-1) * (nx)) for i in range(total_range): if not ((i+1) % nx == 0): # +1 is the shift add_face([i, i+nx, i+nx+1, i+1]) # clockwise print(faces)
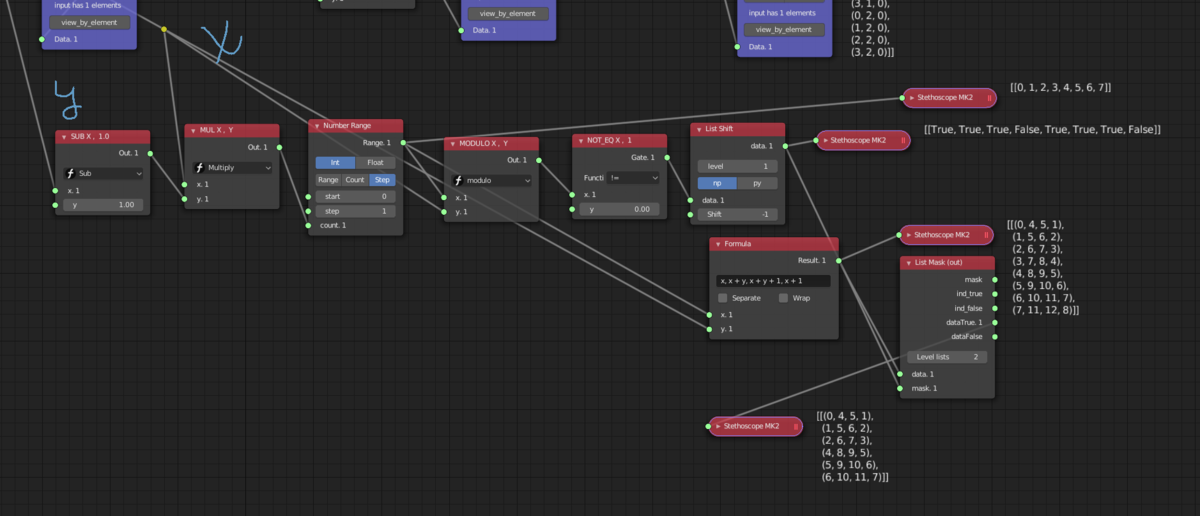
これは基本的なノードを使用した同じアルゴリズムです。類似性がわかりますか?
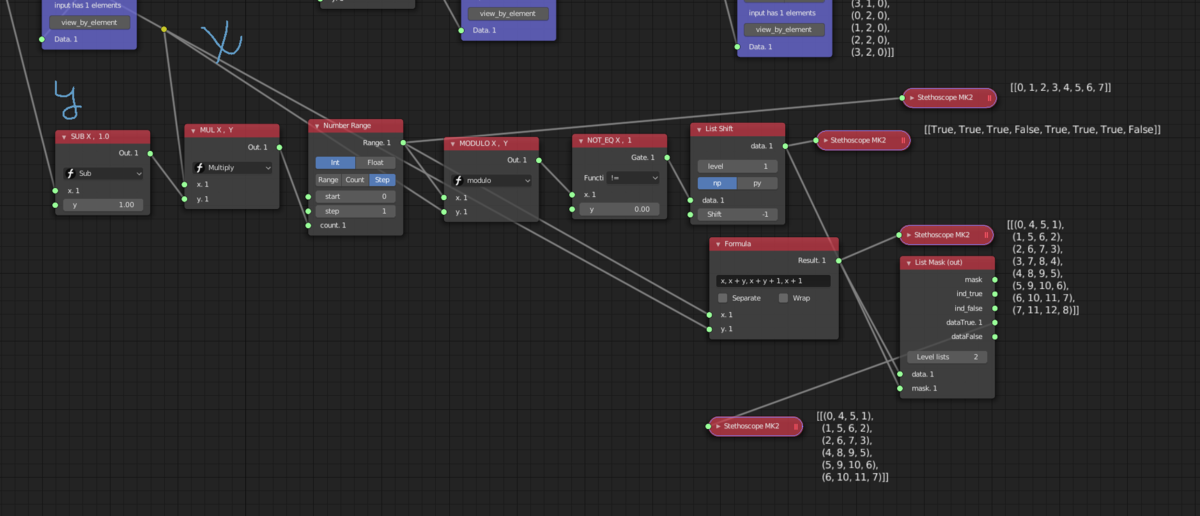
ここでレッスンも途絶えている
最後に
ポリゴンの作成方法がわかったけど、不要なポリゴンを削除する為のアルゴリズムって難しい😭