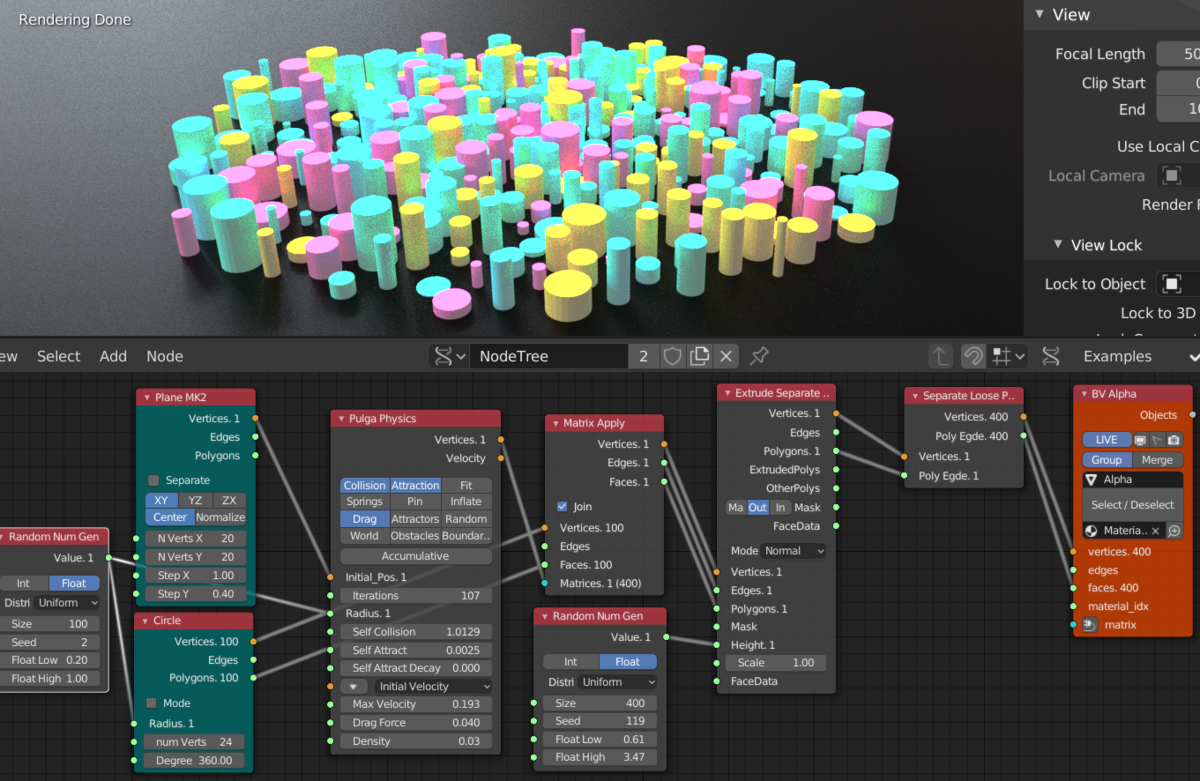
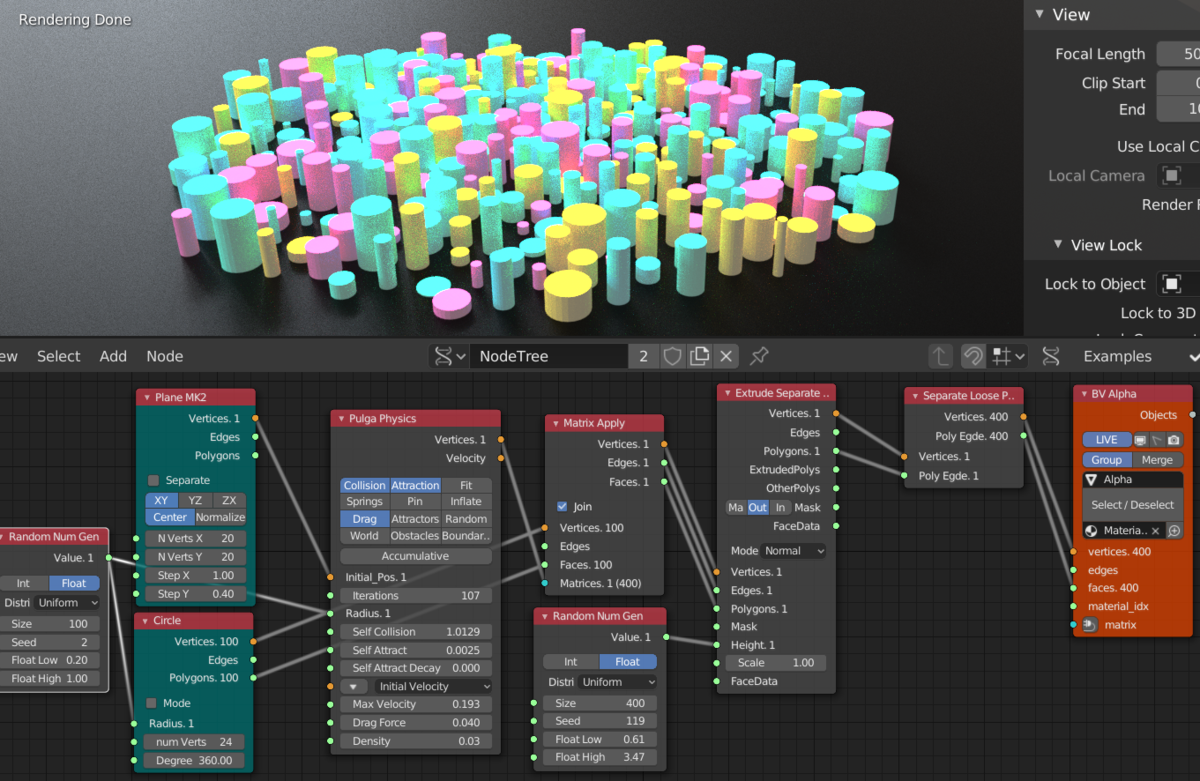
はじめに
Sverchokのサンプルを覗いている時に見かけたノード。
複雑だけど面白そうな事ができそうなノードなので見てみる。
機能てんこ盛りなノードなので今回は一部のみを見る
参照元
機能
このノードは入力パラメータからシミュレーションを作成する。形検索の目的で使用する事を意図しています。これは入力された頂点を与えられた力に反応する球状粒子として使用しシュミレーションを作成する。
このノードはNumpyの基本的な物理システムの実装で、Daniel Shiffmanによる「The Nature of Code」とGrasshopperのKangorooプラグインに強く触発されています。
入力と出力
| 入力 | タイプ | 説明 | 参考リンク |
|---|---|---|---|
| Initial_Pos | Vertices | 元の状態の頂点 | |
| Iterations | Vertices | 処理の反復回数 | |
| Springs | Strings | 頂点を参照する辺 | |
| Springs Length | Strings | Springの長さを指定しする。初期位置から計算する場合は0 | |
| Springs Stiffness | Strings | Spring剛性定数 | 剛性 |
| Pin | Strings | 固定された位置の頂点のインデックス。頂点マスクとインデックス番号を受け入れる | |
| Pin Goal Position | Vertices | 固定された頂点の最終的な位置 | |
| Radius | Strings | 仮想的な球の半径で、交差、質量、表面の計 算に用いられる | |
| Self Collision | Strings | 衝突力。頂点距離 < 半径合計のときに適用される | |
| Self Attract | Strings | 力の大きさを引き寄せる | |
| Self Attract Decay | Strings | 引き寄せる力は距離(力)で減衰する。0 = 減衰なし、1 = 線形、2 = 二次 | |
| Grow | Strings | 半径分散係数。交差してい時に縮小し、していない時に拡大する | |
| Min Radius | Strings | 最小半径制限 | |
| Max Radius | Strings | 最大半径制限 | |
| Pols | Strings | 頂点を参照するポリゴン。(膨張力の計算に使用する) | |
| Inflate | Strings | 力の大きさを膨張する(面毎) | |
| Initial Velocity | Vertices | 初期頂点速度 | |
| Max Velocity | Strings | 最大頂点速度 | |
| Drag Force | Strings | 環境からの運動抵抗 | 抗力 |
| Attractors | Vertices | アトラクター(引きつけるもの)の原点 | |
| Attractors Force | Strings | アトラクターのひきつけ力の大きさ | |
| Attractors Clamp | Strings | アトラクターの最大影響距離 | |
| Attractors Decay | Strings | ひきつけ力の減衰。0は減衰なし、1 = 線形、2 = 2次 | |
| Random Seed | Strings | ランダムシード数 | |
| Random Force | Strings | ランダムな力の大きさ | |
| Random Variation | Strings | ランダムな力の変化 | |
| Density | Strings | 粒子密度 | 粒子密度 |
| Gravity | Vectors | 質量に依存しない一定の力 | 重力 |
| Wind | Vertices | 質量に依存する一定の力 | 風 |
| Bounding Box | Vertices | システムの有効範囲を示す境界。与えられた頂点のバウンディングボックスで動作する(最小は2つ) | |
| Obstacles | Vertices | 障害物の頂点 | |
| Obstacles Pols | Strings | 障害物の頂点を参照するポリゴン(三角形である必要がある) | |
| Obstacles Bounce | Strings | 障害物のバウンス能力 |
累積
アクティベートされた時、すべての NodeTreeは前回の更新を開始点として使用します。この更新は更新ボタンや定期的な更新をするトリガーイベント(アニメーションの作成や値の変更など)によってトリガーされます。
いくつかのオプションを提供しています。
- Reset システムを初期状態に戻します
- Update 1つのノードツリーを更新します
- Pause ノードの計算を停止しUIの変更を無視します
使用例
公式には複雑な例が多くあるのでそちらも見てください
Attractor 引きつけ
初期状態
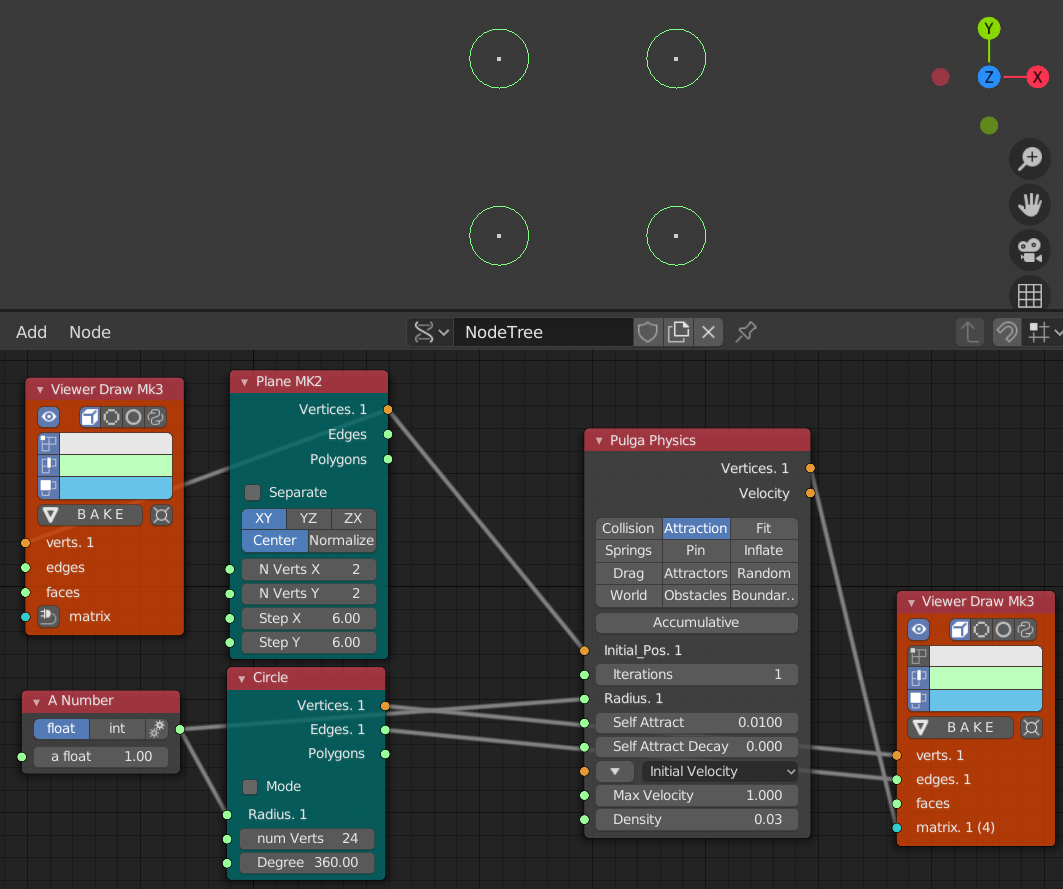
- 4つの円を配置している
- Self Attract(引きつける力) = 0.01
- Iterations = 1
Iterations 反復 と Self Attract 引きつけ力 と Self Attract Decay 引きつけ力減衰
反復数(Iteration)はシミュレーションを行う回数で、1となっている。
反復数を増やすと引きつけ力(Self Attract)と与えられた半径に応じて円が引き合う
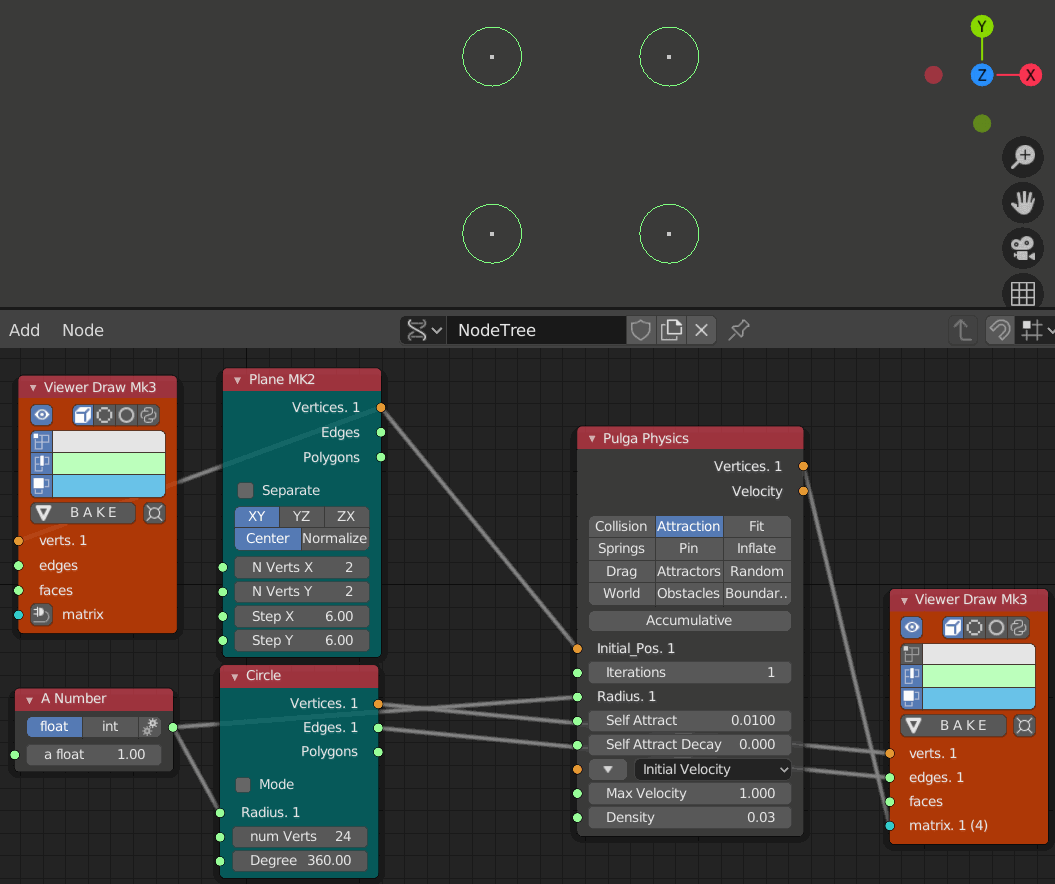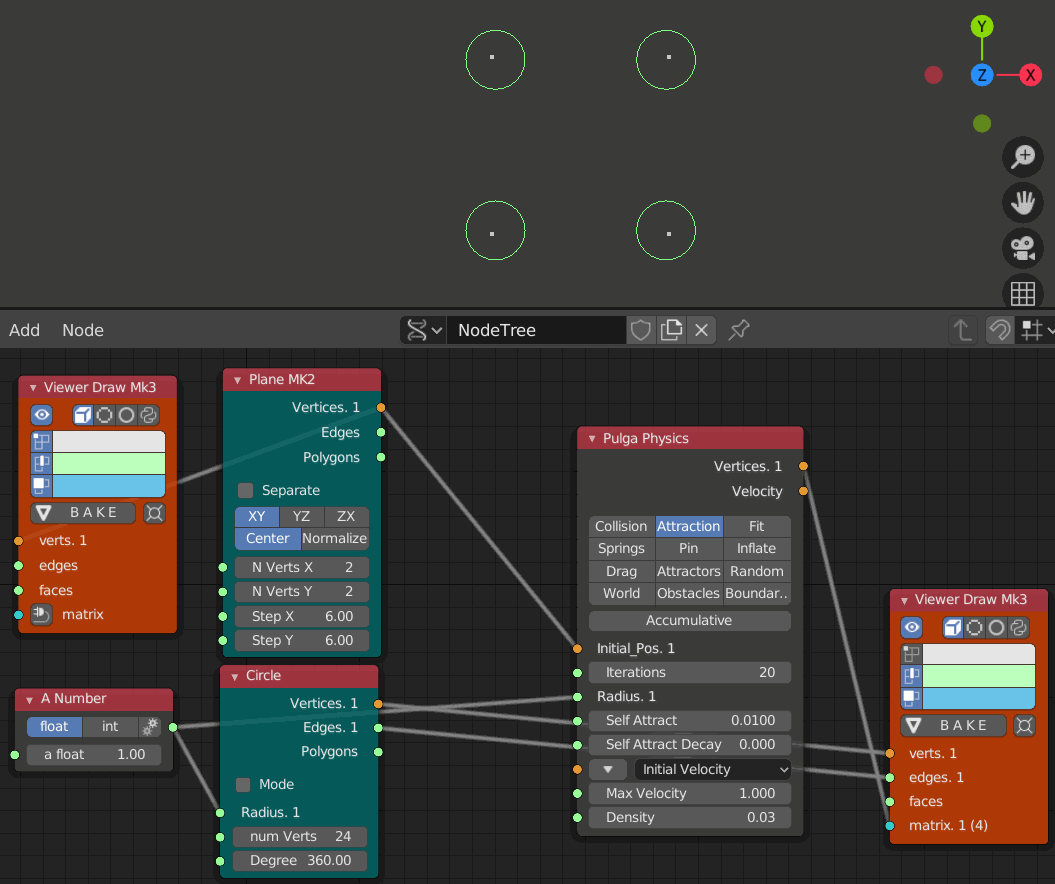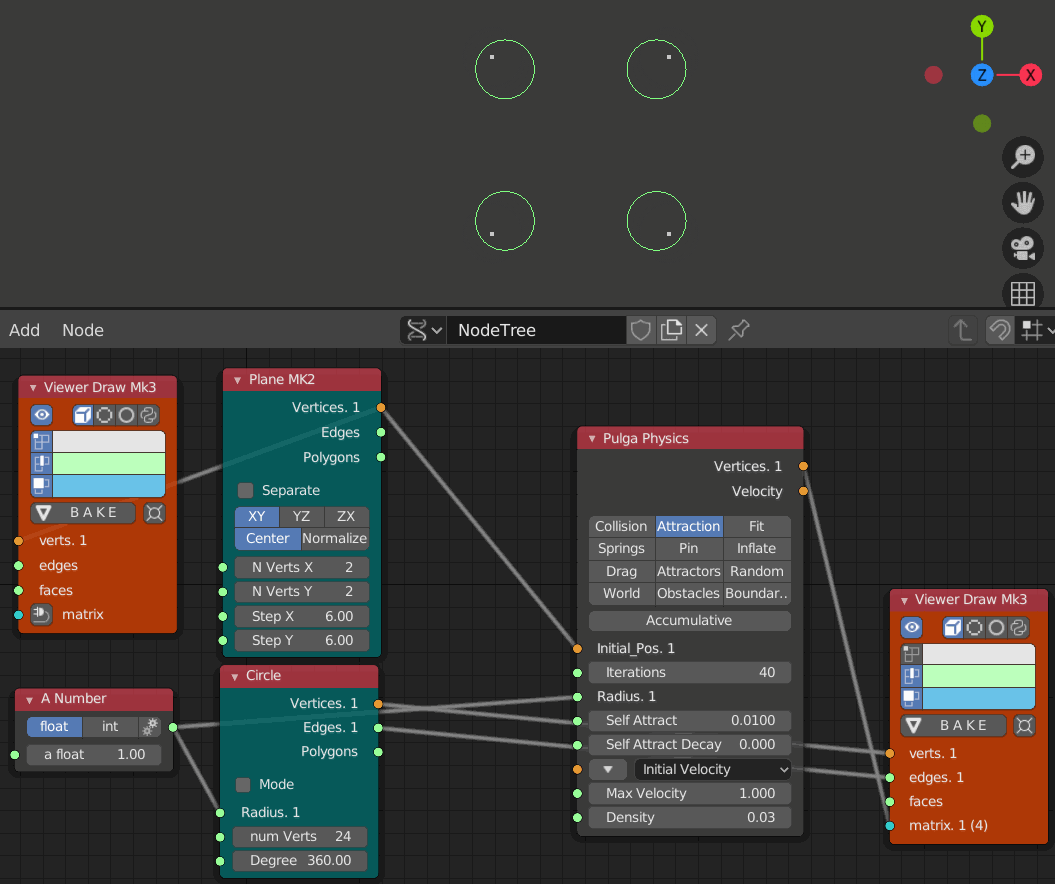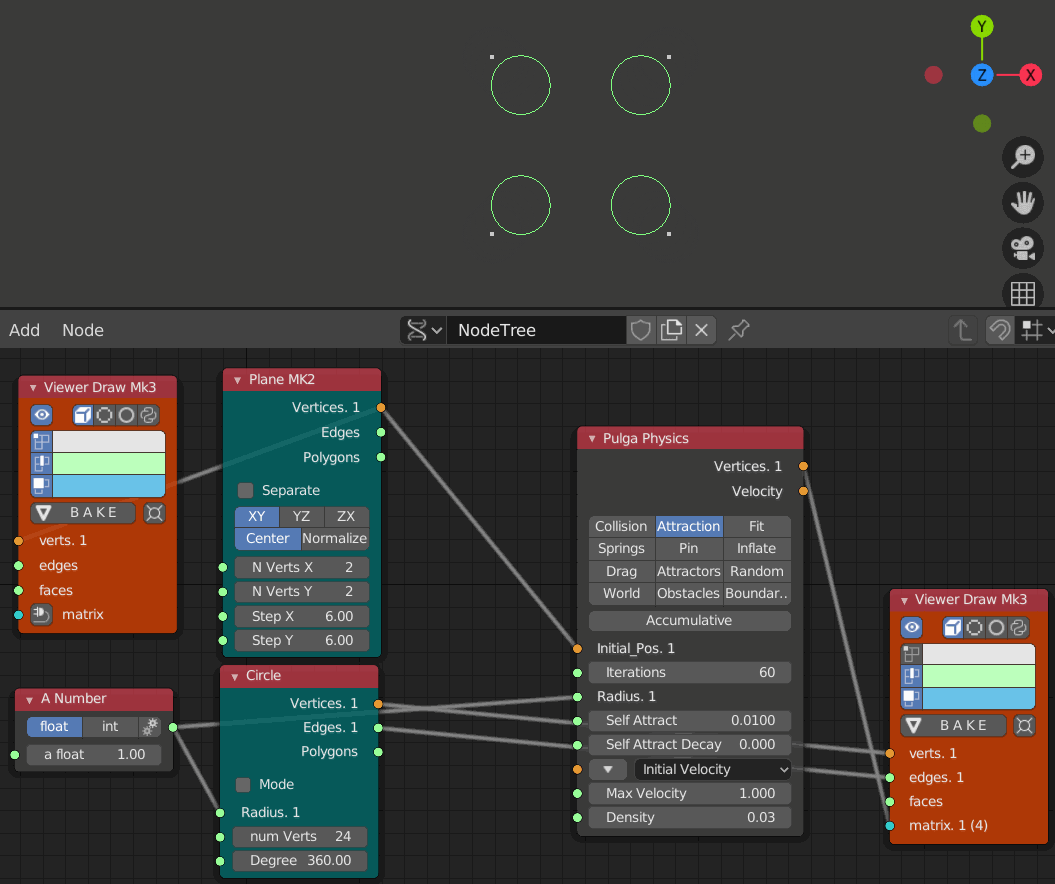
- iteration 1, 10, 20, 30, 40, 50, 60のステップ
- Self Attract = 0.01
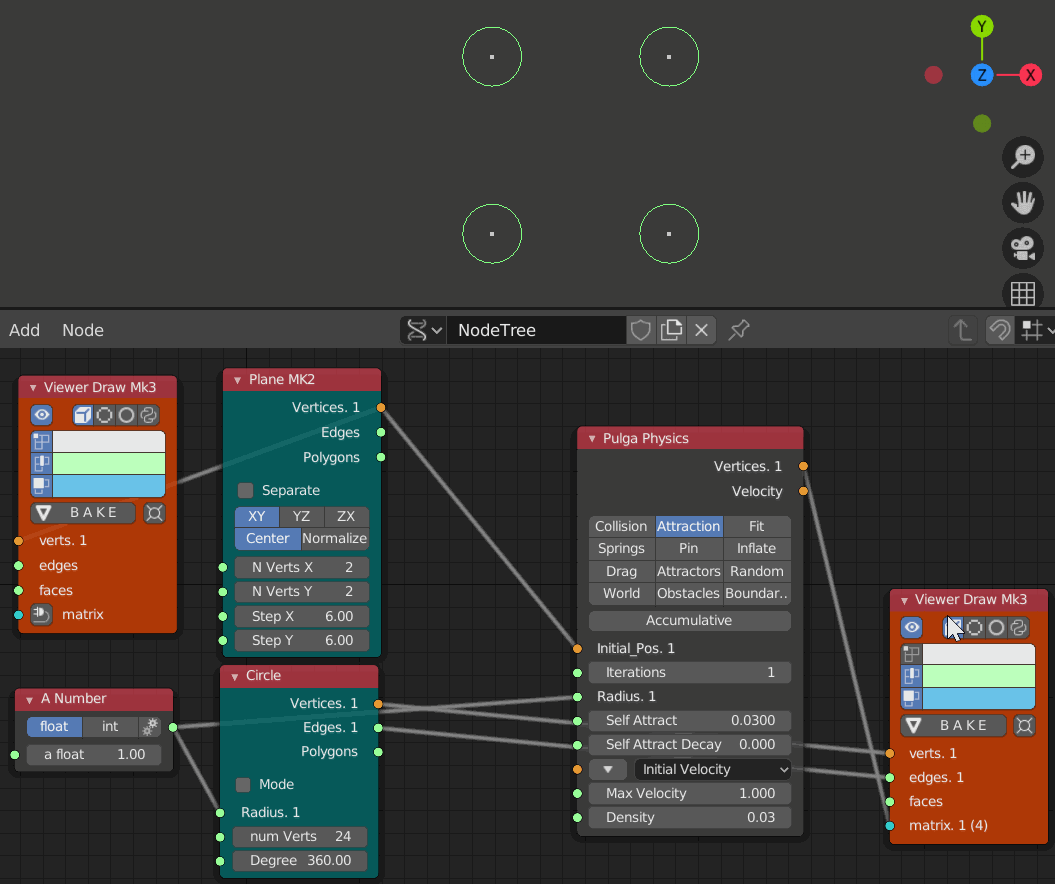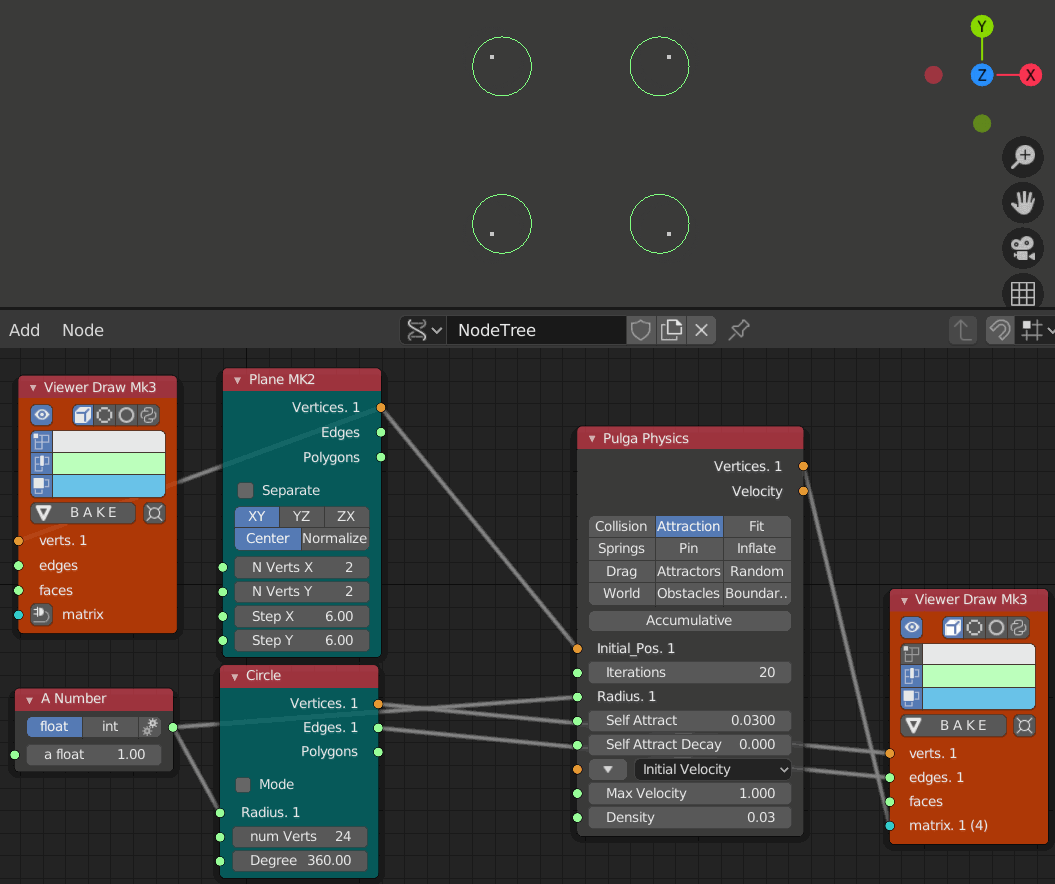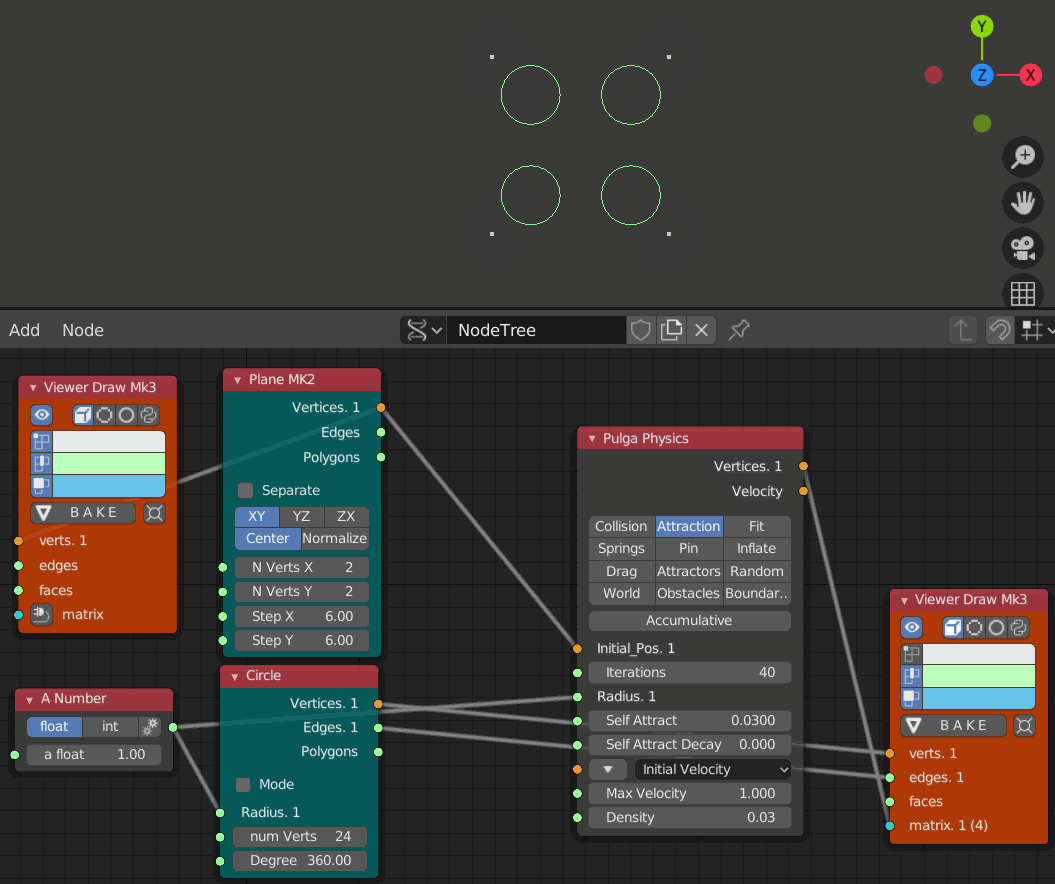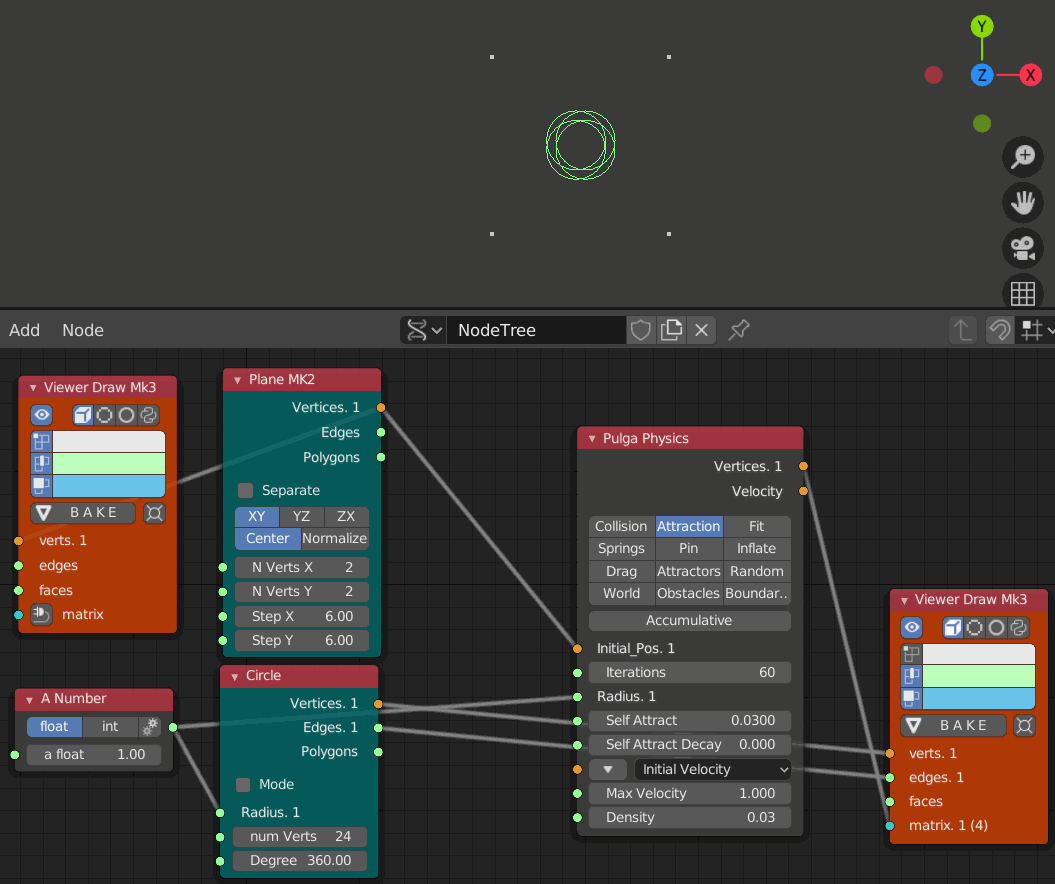
- iteration 1, 10, 20, 30, 40, 50, 60のステップ
- Self Attract = 0.03
引きつけ力を0.01から0.03に変えると強く引き合っている事がわかる
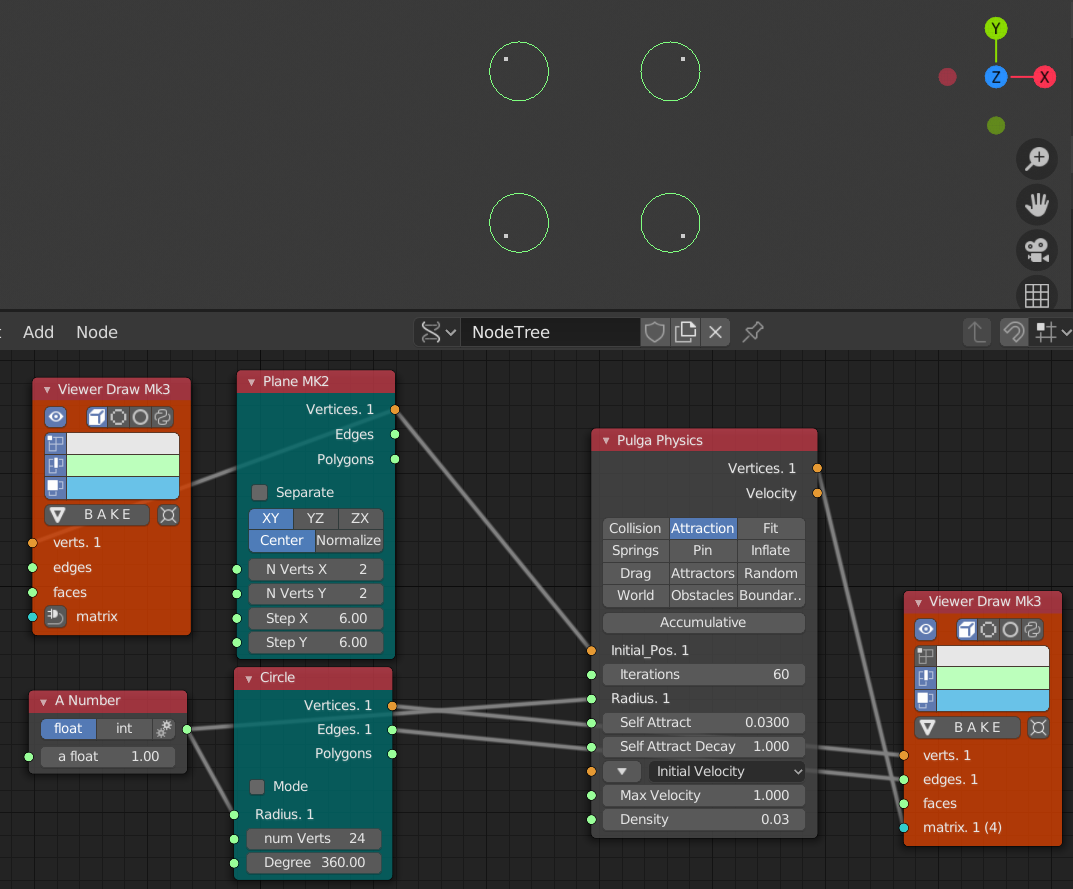
- Self Attract Decay を 0 から 1 に変更
上記以外は一個前の例と同じパラメータで反復数が60の例だが、引きつける力が弱くなっている。
半径を変える
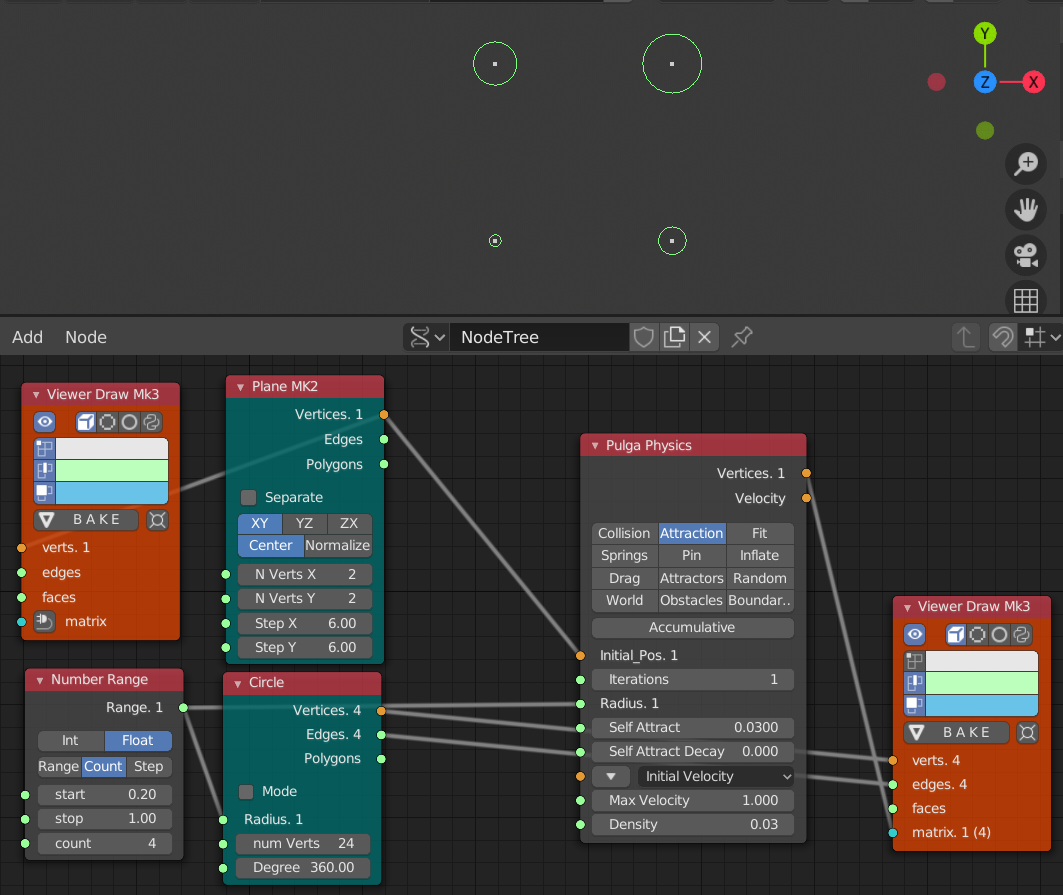
- 0.2 から 1までで徐々に大きくなる円を作成
- Pulga Physics の Radius にもその数列を接続している
- Self Attract 0.03
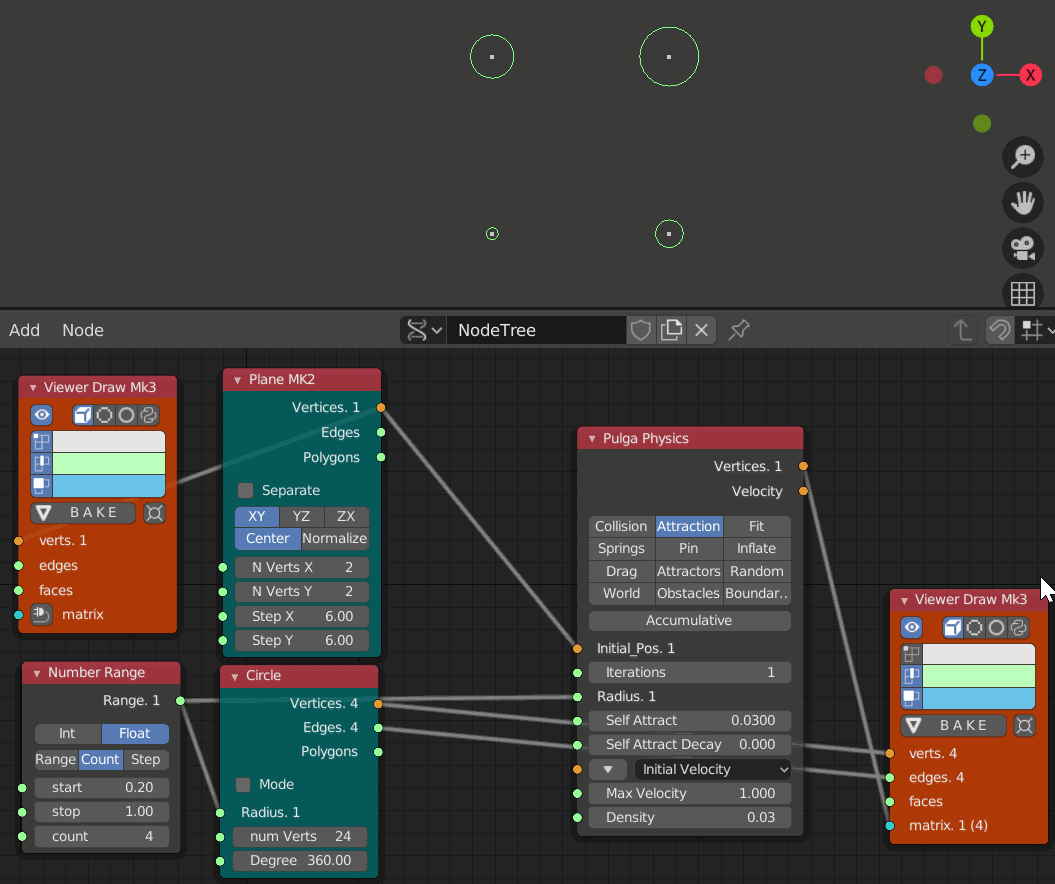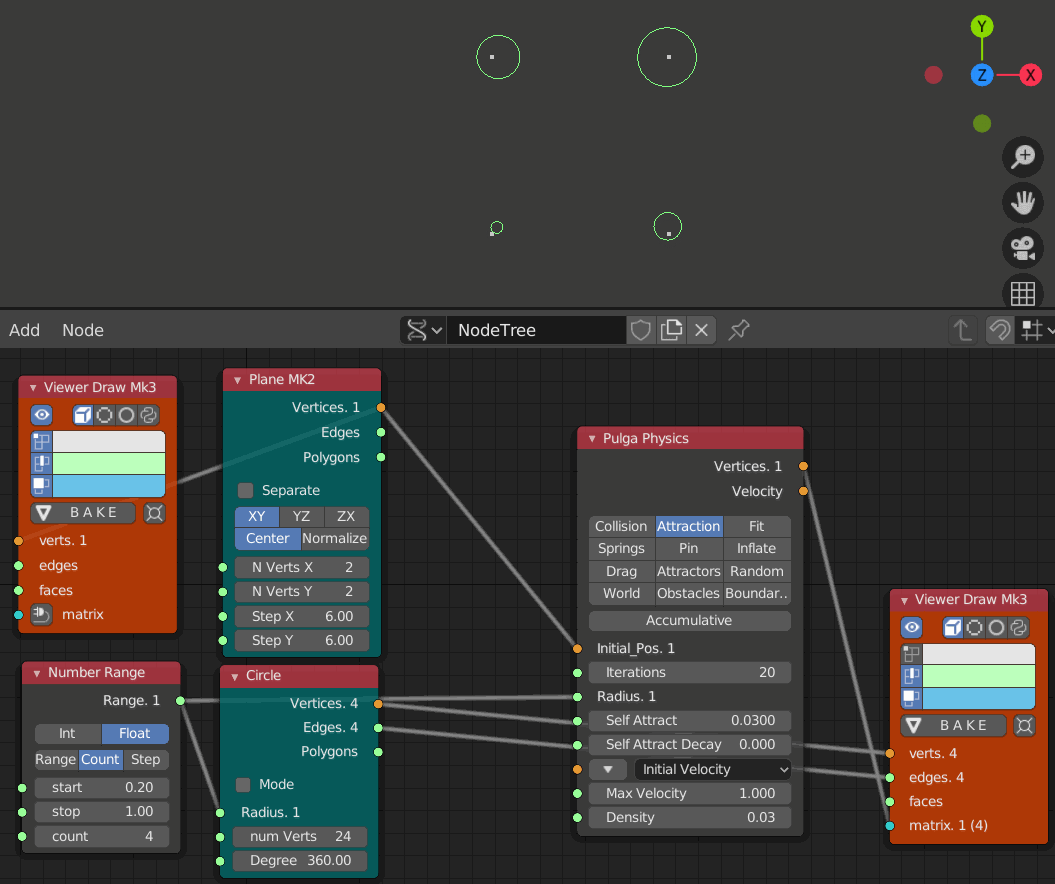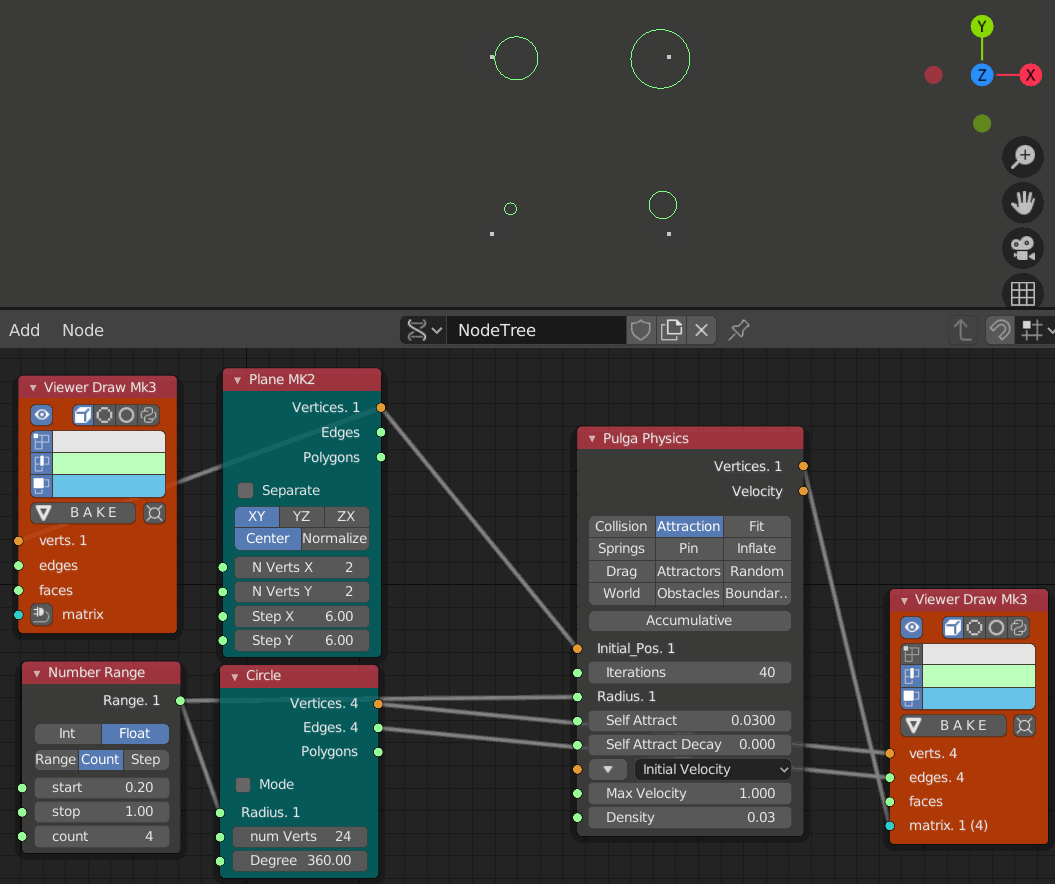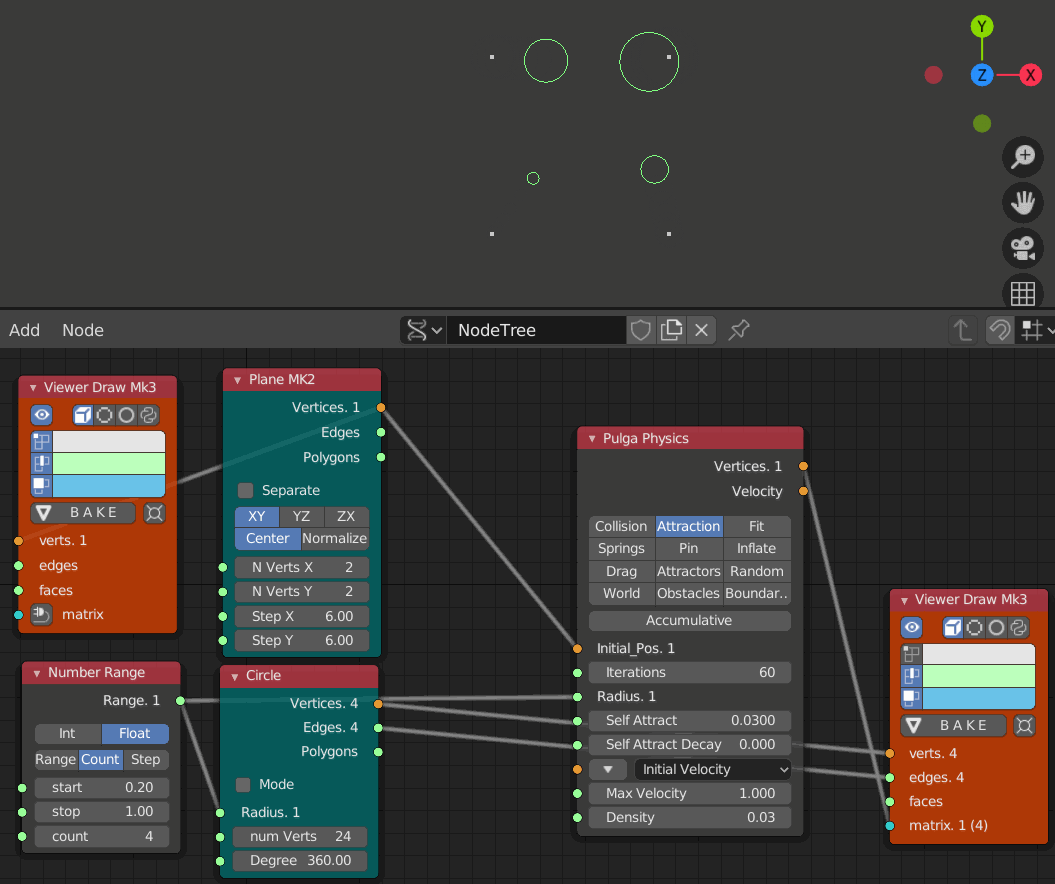
- iteration 1, 10, 20, 30, 40, 50, 60のステップ
小さな円ほど大きな円に寄っていっており大きな円は初期位置をあまり動いていない。
2つの物体の間には、物体の質量に比例し、2物体間の距離の2乗に反比例する引力が作用する
万有引力 – Wikipedia
万有引力の解説にある通り、この引きつけるものが大きいほど引力が強くなる様子。
Collision(衝突)
初期状態
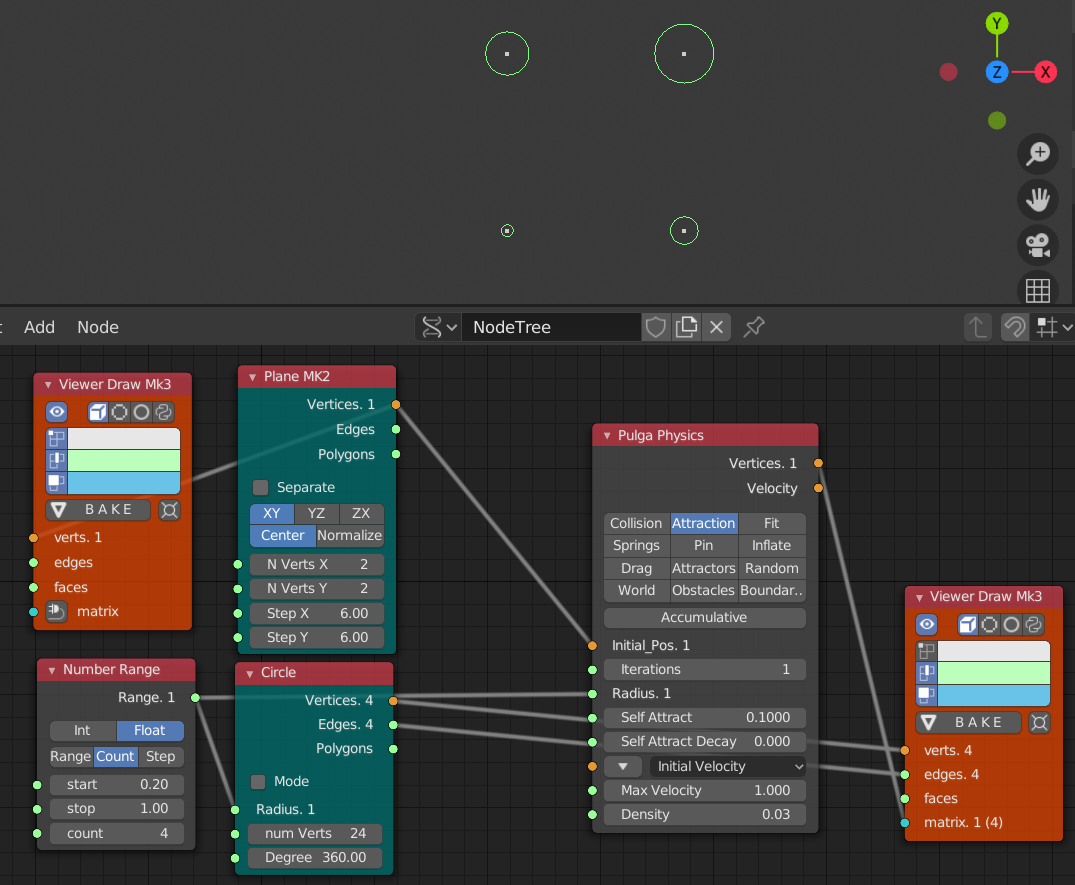
- Self Attract 0.1
- Collisionなし
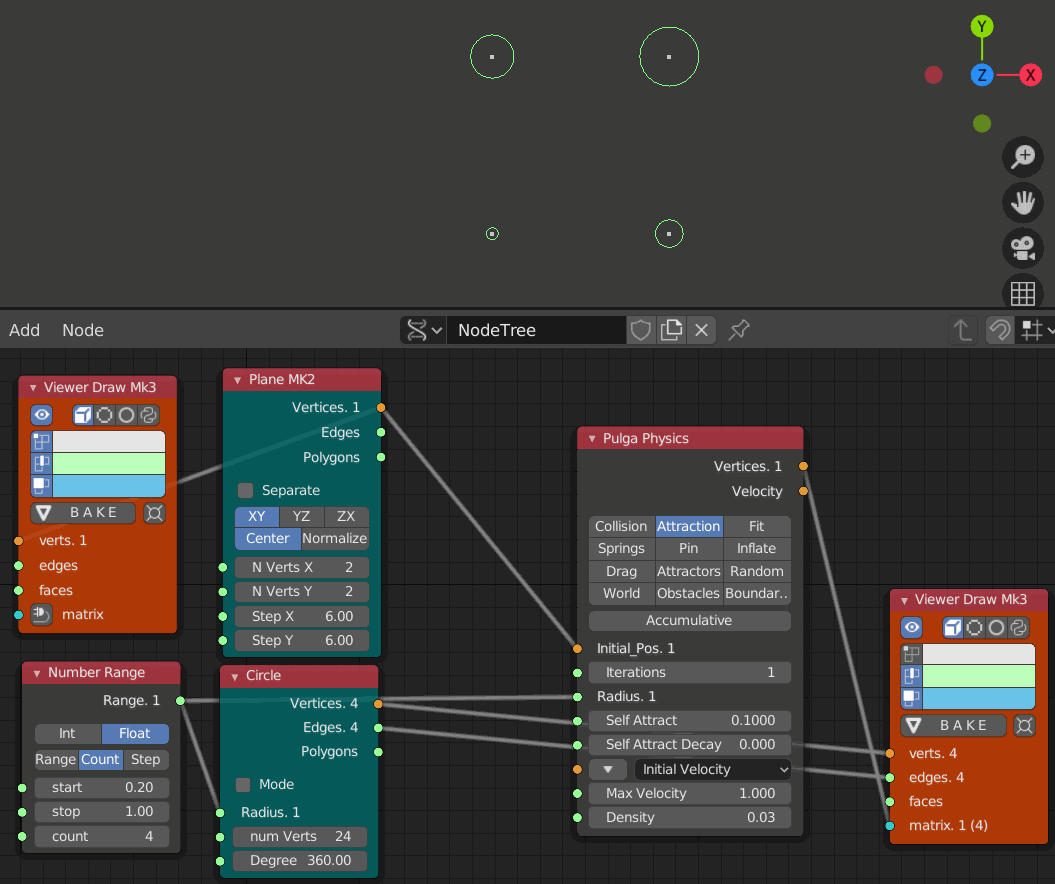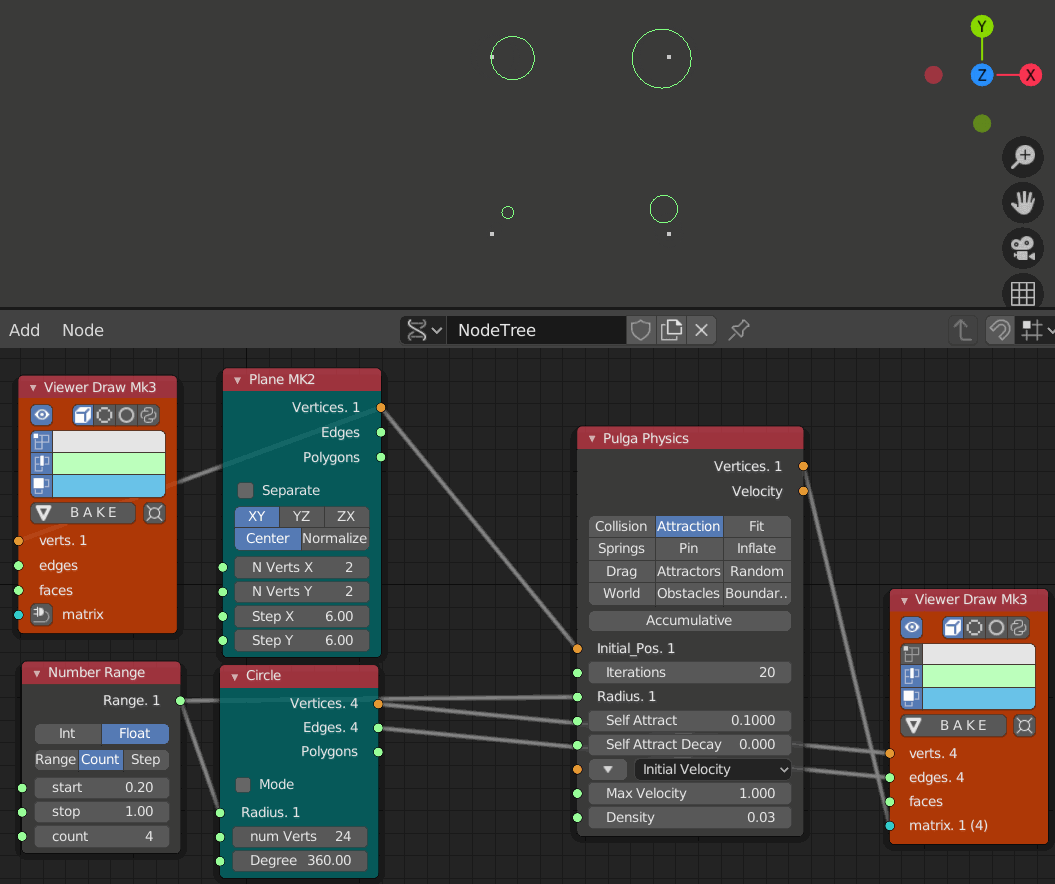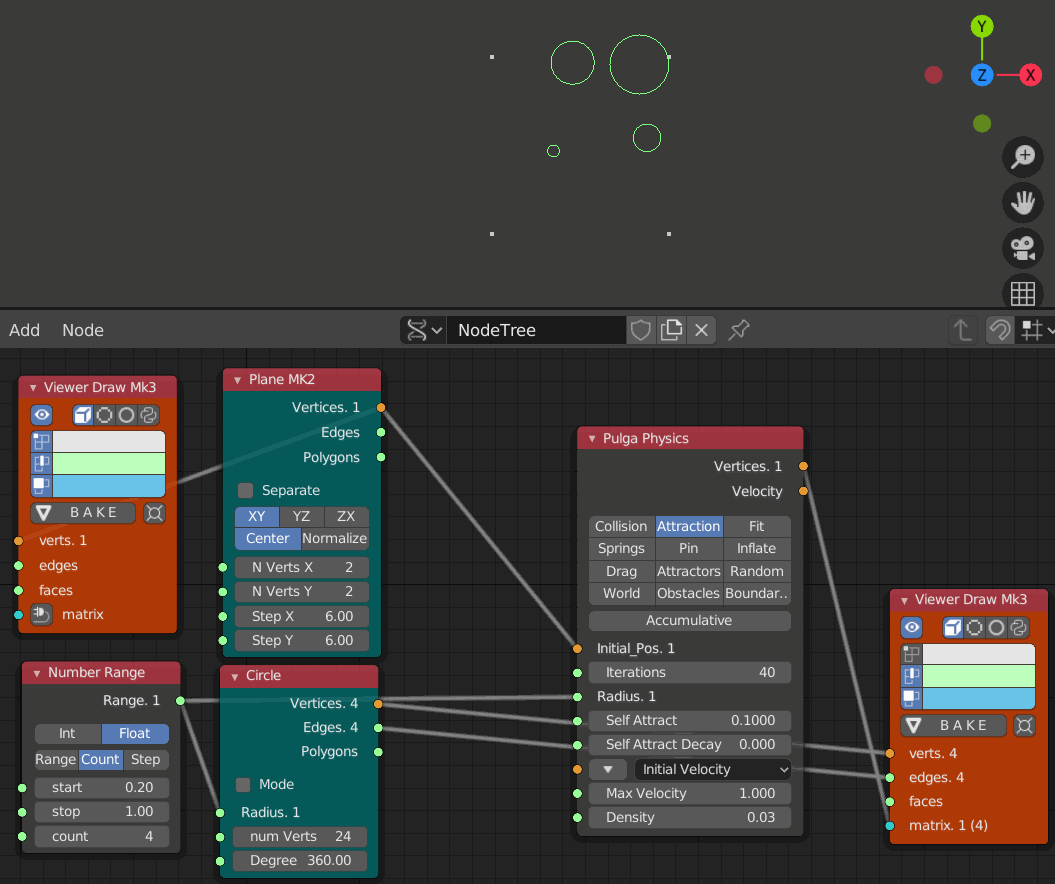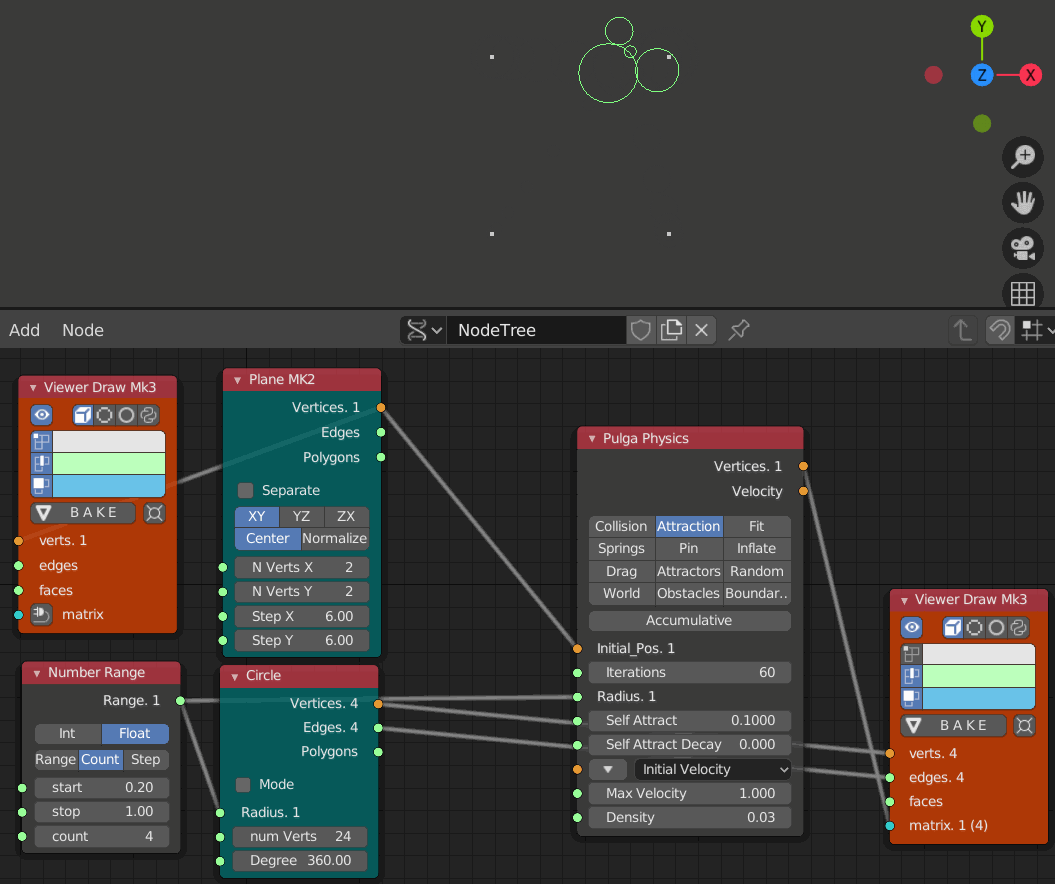
- iteration 1, 10, 20, 30, 40, 50, 60のステップ
円はIteration60辺りで交差している
衝突あり
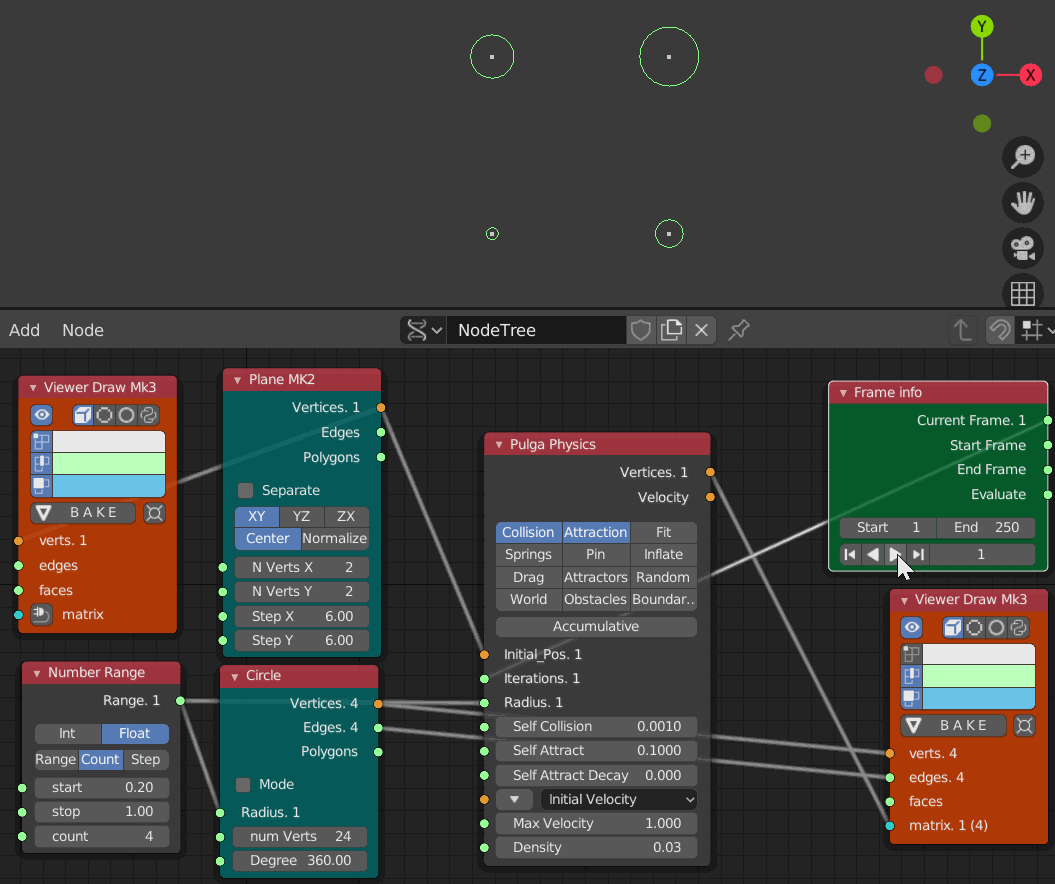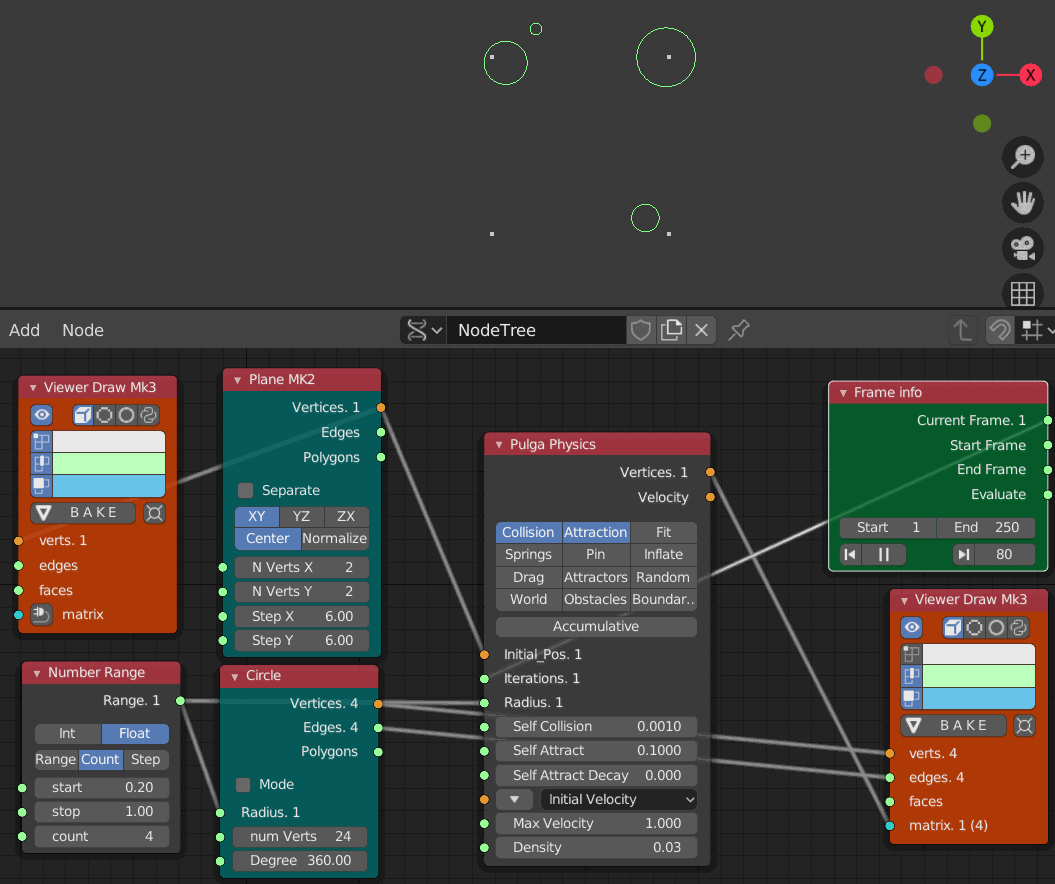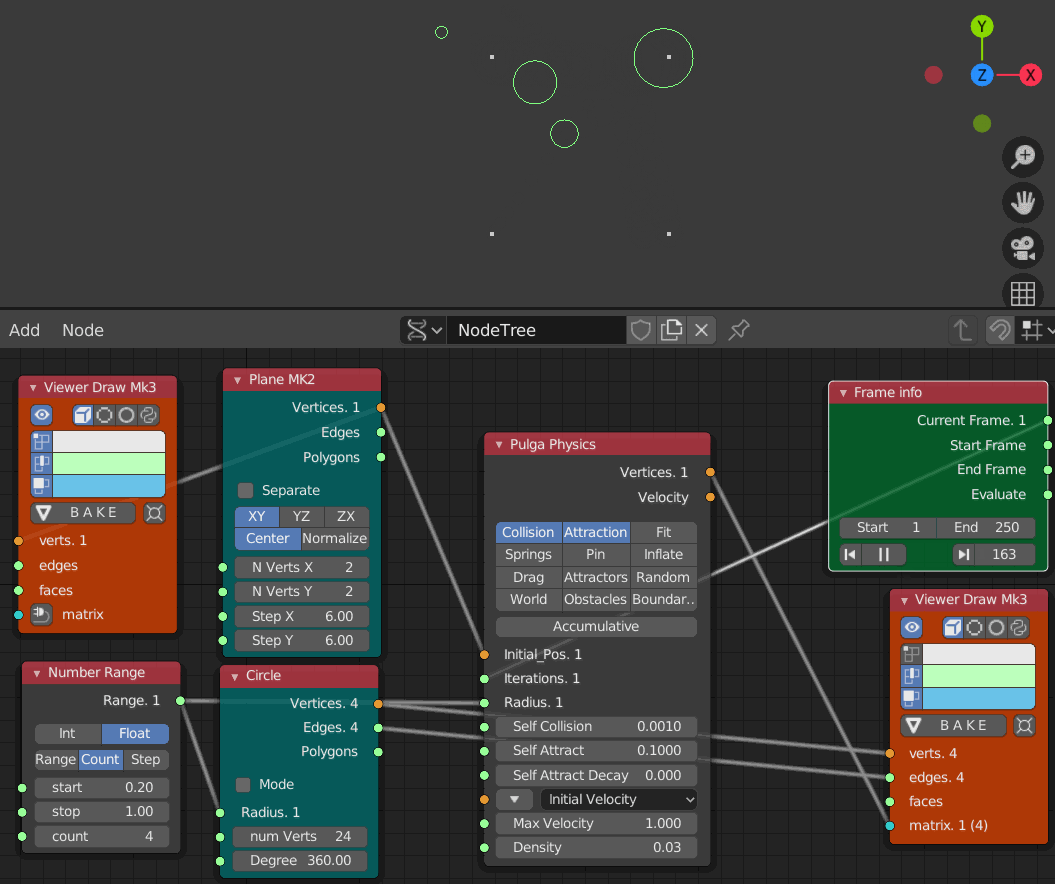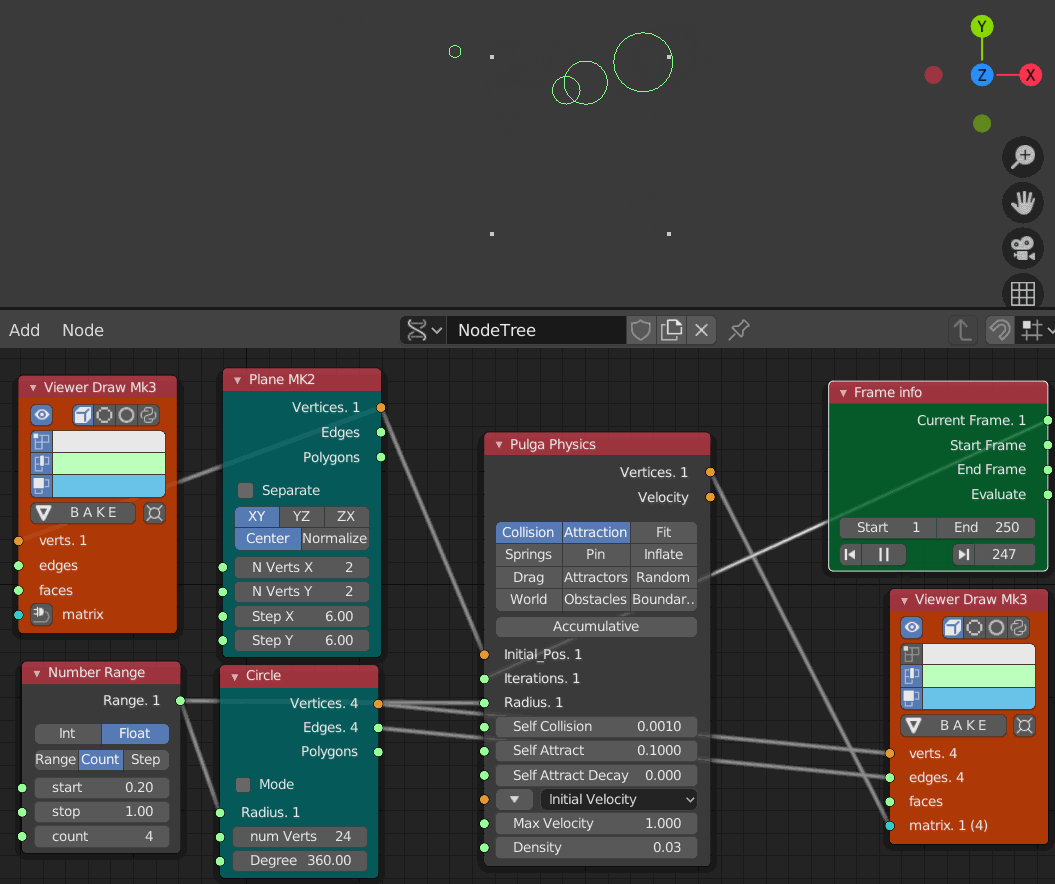
- Collision 0.001
- Iteration 1 から 250までのアニメーション
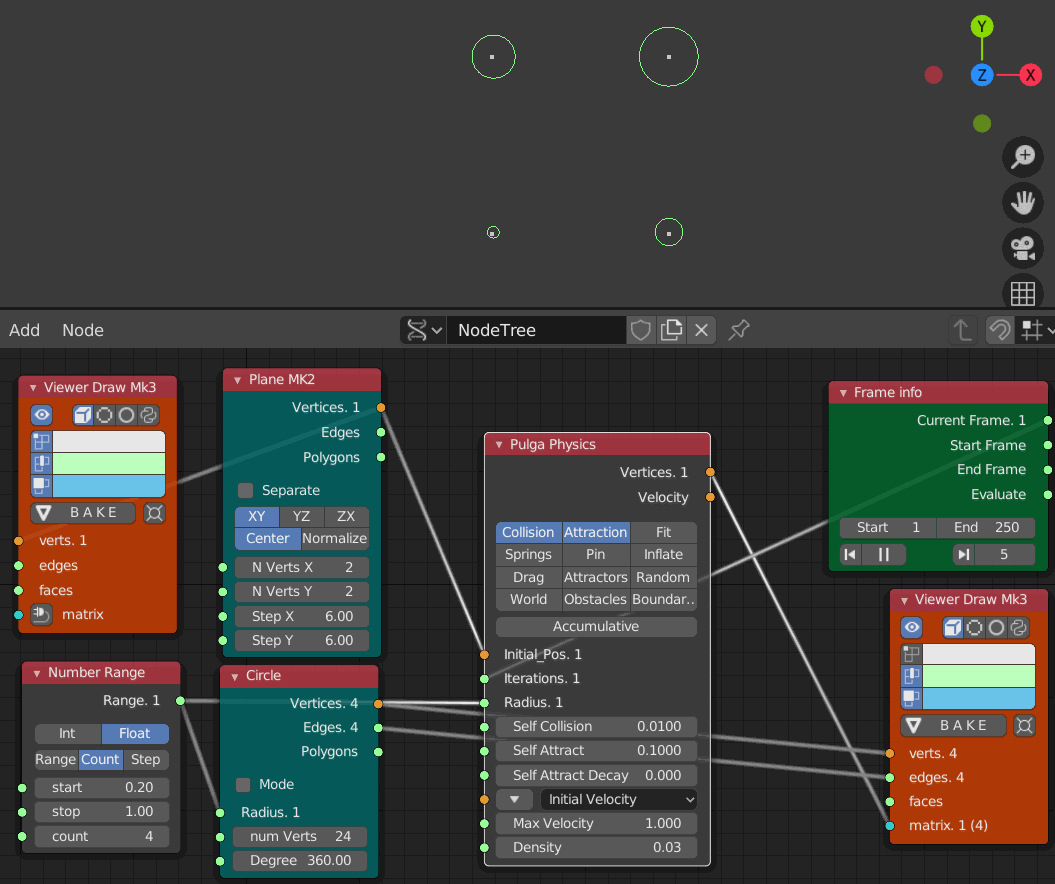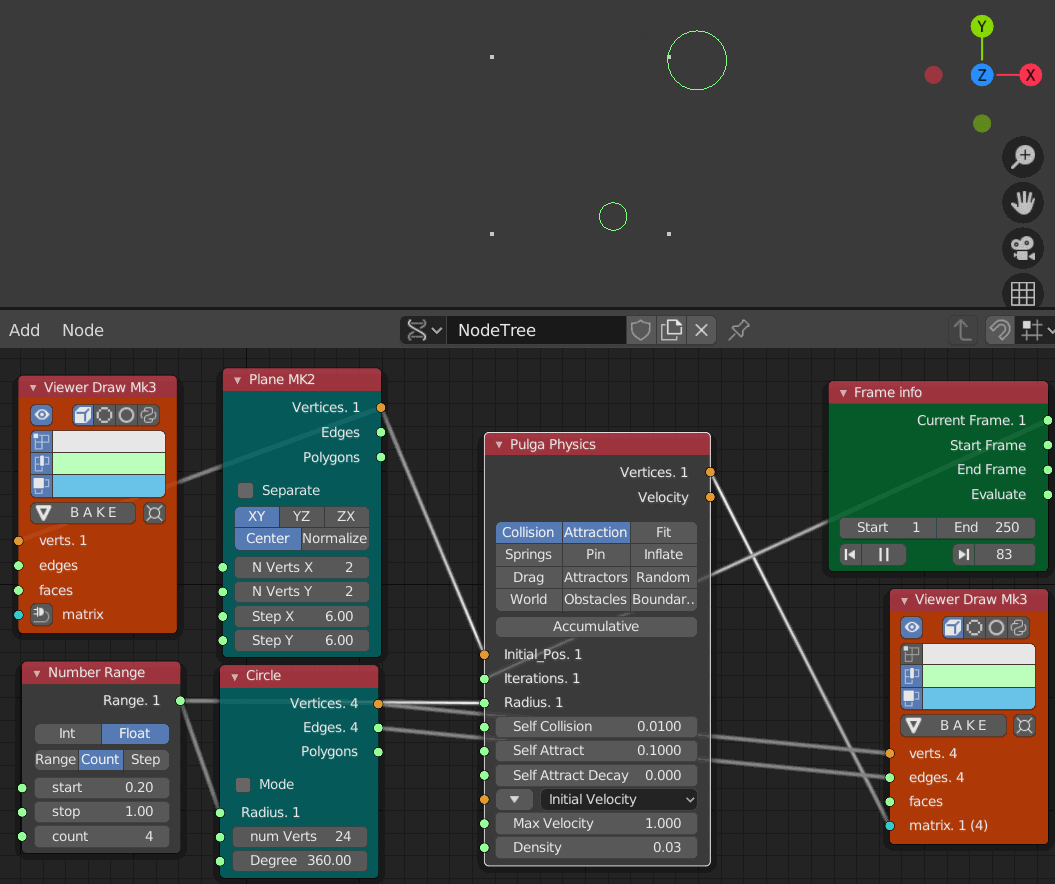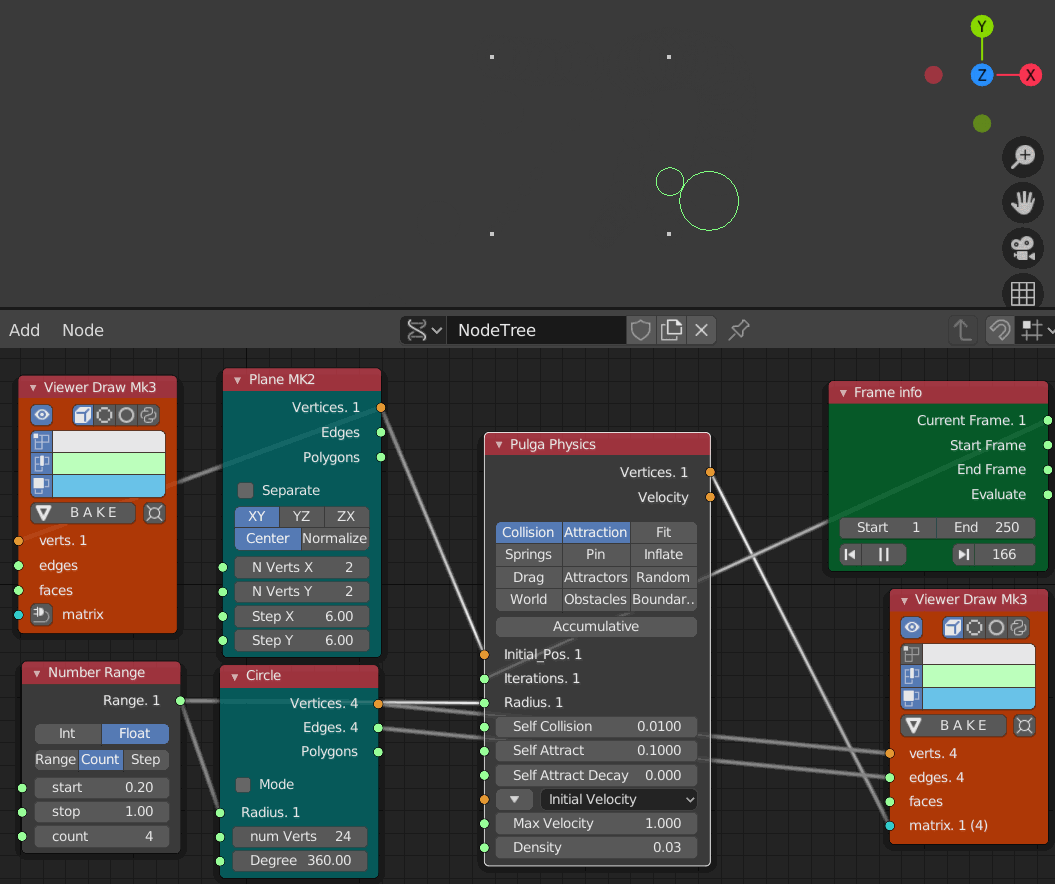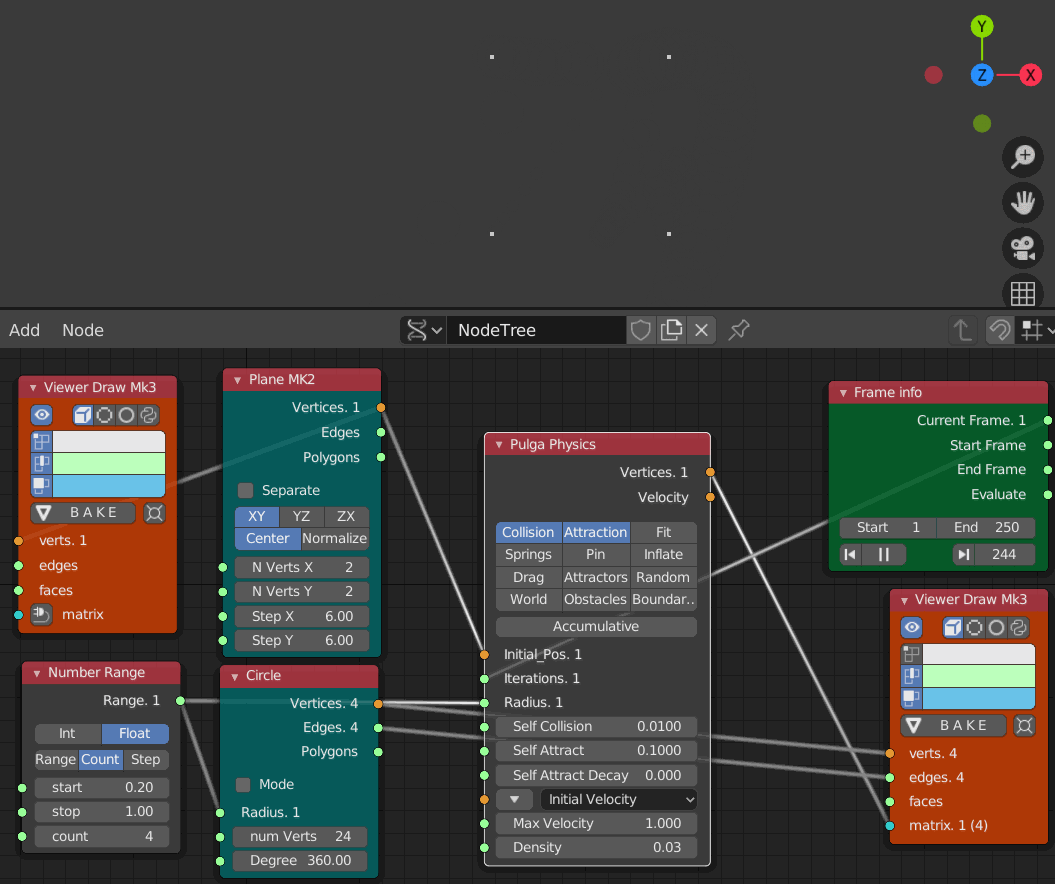
- Collision 0.01
- Iteration 1 から 250までのアニメーション
Collisionが大きいほど衝突した時の衝撃も強い様子
Drag Force 抗力
初期状態
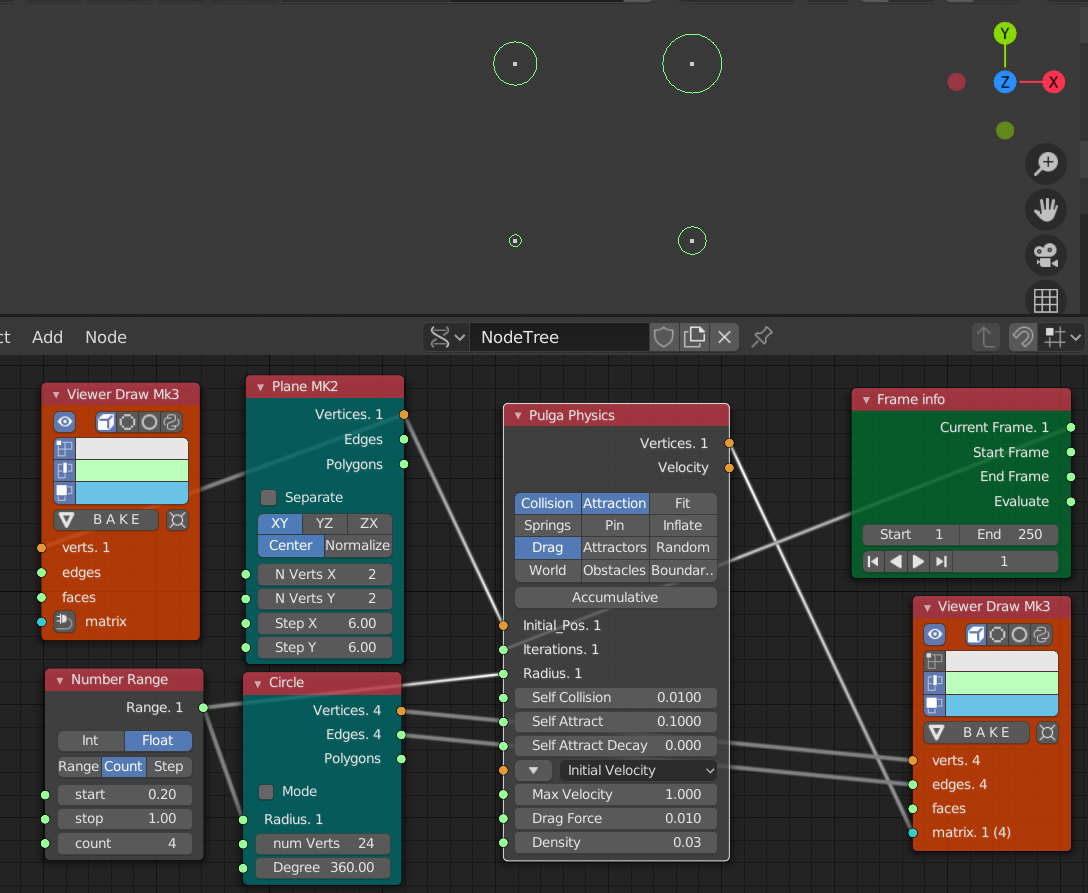
- Self Collision 0.01
- Self Attract 1
- Drag Force 0.01
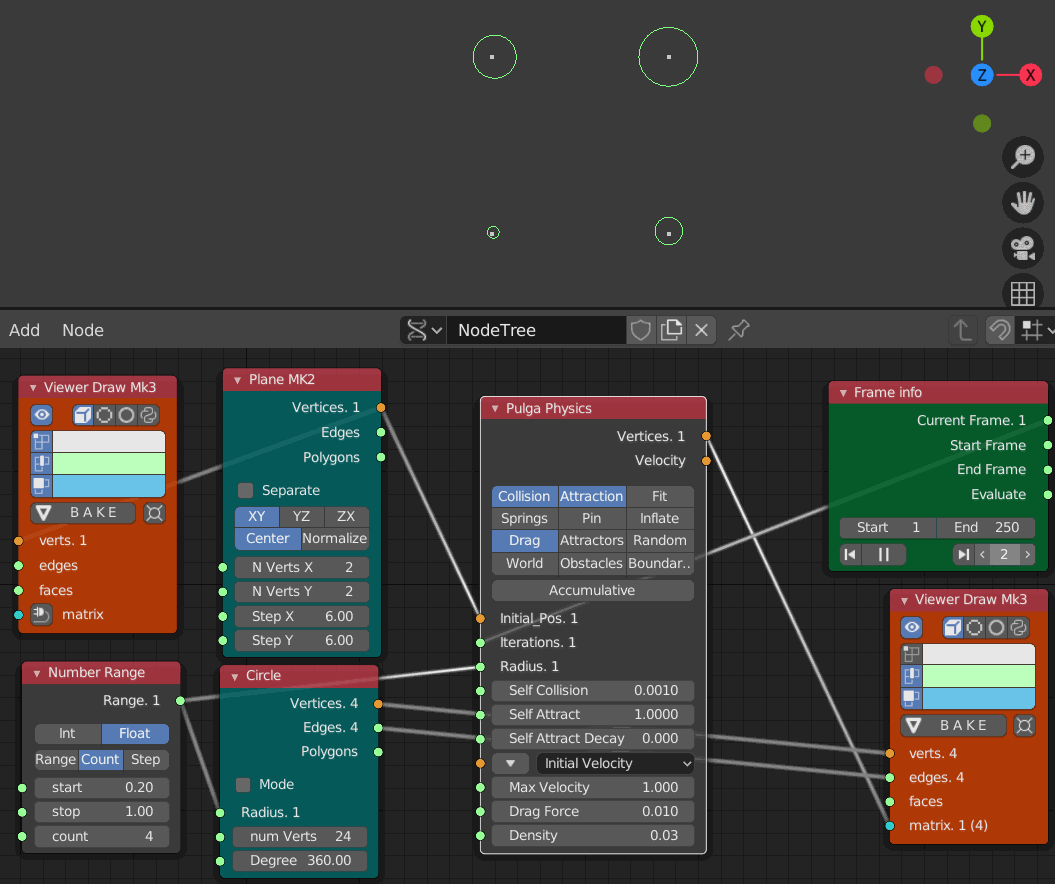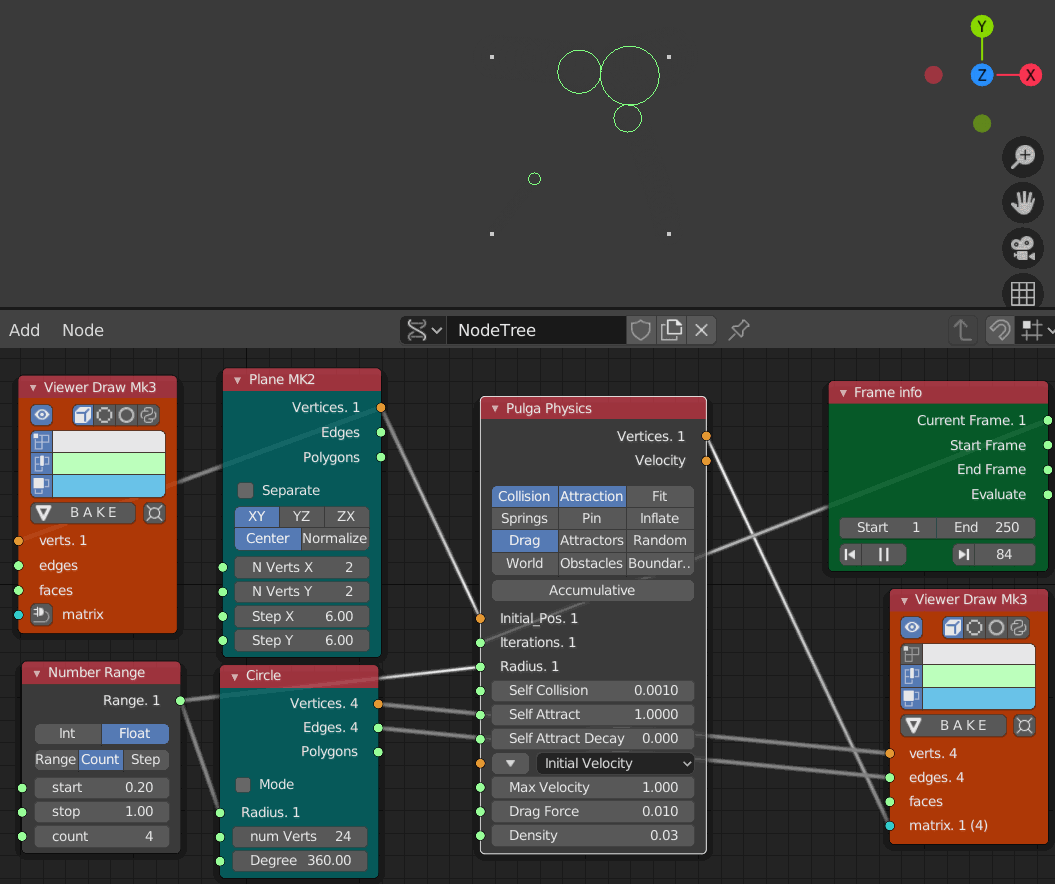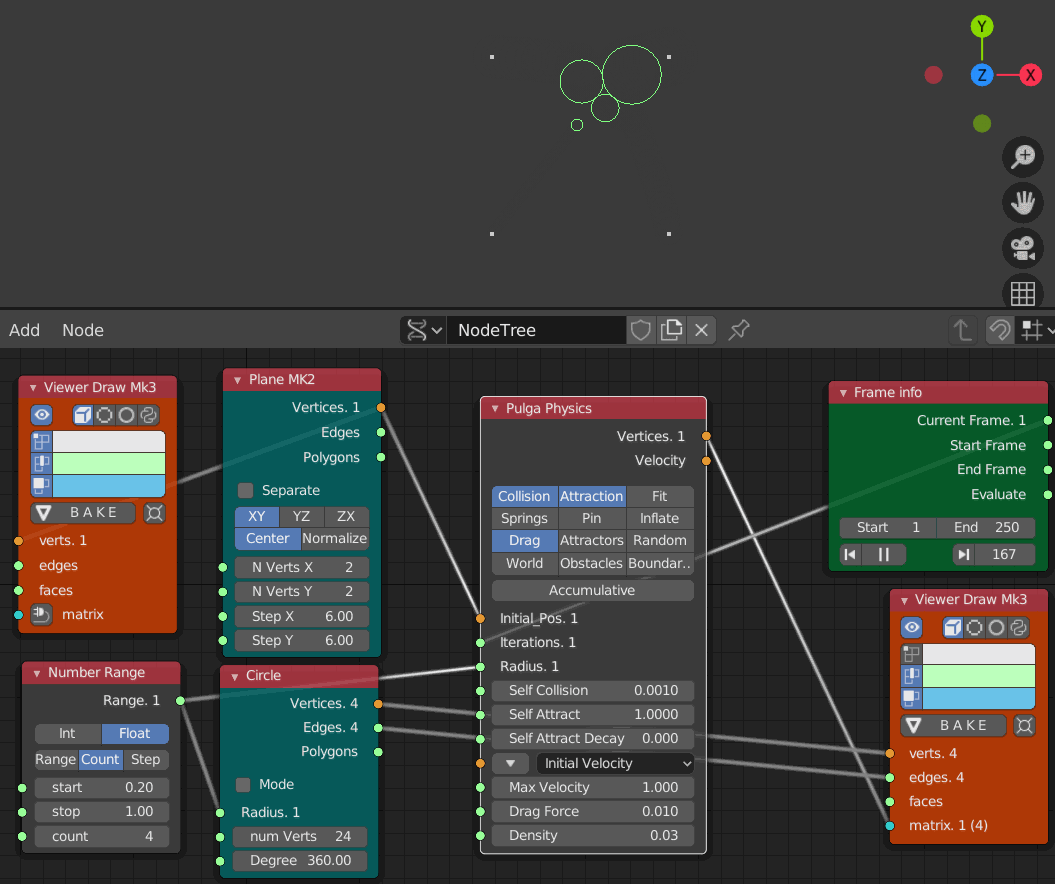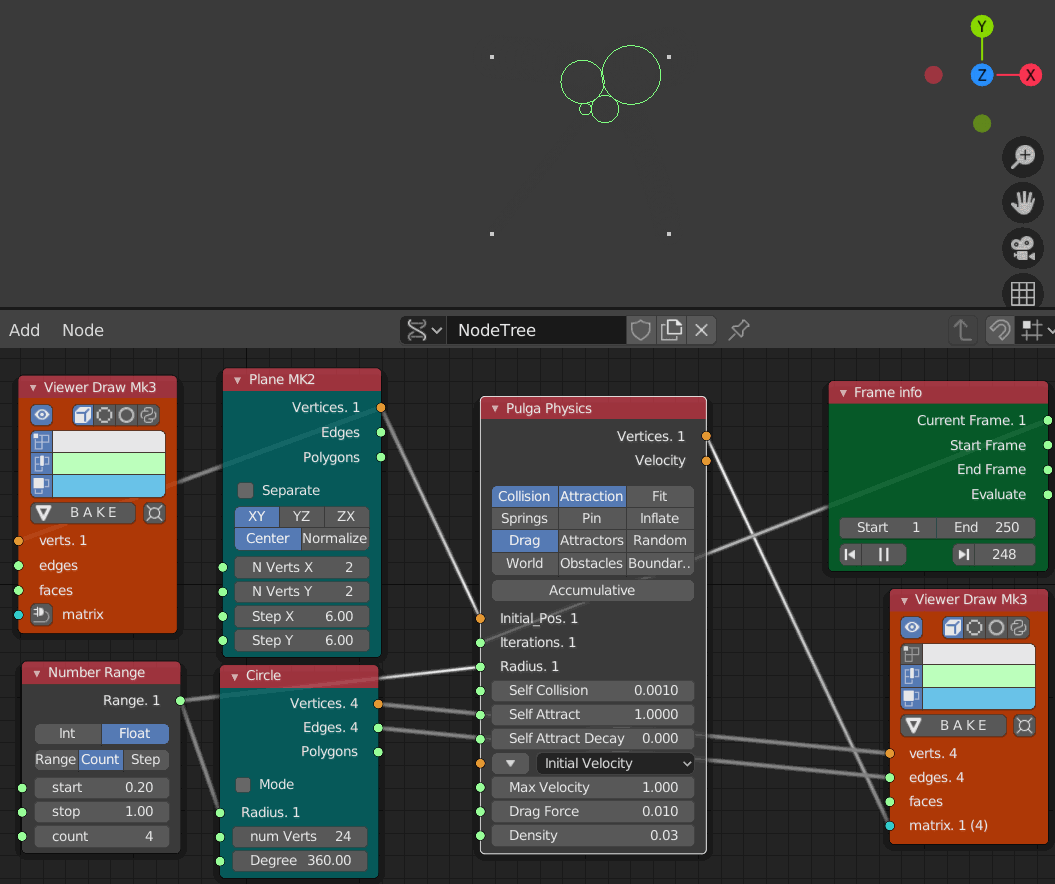
- Iteration 1 から 250までのアニメーション
衝突しても前の例ほどそれぞれの円が吹き飛んでいない事がわかる。この抗力と衝突と引きつけ力のバランスで磁石のようにくっつき合うものが出来上がるみたい。
最後に
このノードだけでもすごい機能数。Sverchok恐るべし