はじめに
最近Curve、Surface、Vector Fieldというものが登場した。
これらの理解をするために、この中では一番単純であろうCurveのドキュメントを見てみる
参照元
Curve
SverchokではCurveという言葉をほとんど数学で使用されているCurveと同じように使います。
ユーザー視点では、Curveオブジェクトは3D空間に配置されたただの(荒いまたは滑らかな)曲線で、始点から始まり終点曲線の始点と終点へ行きます。この始点と終点は一致する場合があり、そのような場合はClosed(閉じている)やCyclic(周期的である)と言えます。
Sverchokの文脈でこの用語を理解するために、Curveオブジェクトのいくつかのプロパティを見てみましょう。
- 曲線は有限、一次元オブジェクト、3D空間に存在している
- すべての曲線は必ず2つのエンドポイントを持つ。それより多くも少なくもない
- エンドポイントが一致している場合、曲線は閉じていると考えられる
- エンドポイントが3つ以上生じる場合がある為、曲線の内側に隙間がない場合があります。
- 曲線の内側でエンドポイントが一致している場合を除いて、曲線には分岐点は無いでしょう。
数学的には、曲線は3次元空間の点の集合でありRからR3まである関数のコドメインとして定義する事が出来ます; すなわち関数は実数を3D空間のベクトルへマップ(写像)します。私達は”充分な”関数だけを考えていきます。より正確に言えば、そのような関数は連続的であり、各点で少なくとも3つの導関数を持っています(ほとんどの場合)
各曲線が1つ以上の関数から定義できる(これは曲線のパラメータ化と言われます)ということを理解しておくのは重要です。通常、特定のタスクにおいて一番目的に適合したものを使うでしょう。
通常私達は t という文字をパラメータに使います; u を使う場合もあります。
例えば、(0, 0, 0) で始まり (1, 1, 1)で終わる直線を考えましょう。下記のパラメータ化はすべて同じ線を定義しています
x(t) = t y(t) = t z(t) = t
x(t) = t^2 y(t) = t^2 z(t) = t^2
x(t) = t^3 y(t) = t^3 z(t) = t^3
お分かりでしょうが、そのための方程式は好きなだけ書けます。
同じ曲線に対して異なったパラメータ化は、曲線の始点と終点に対応する t パラメータの値が異なる場合があります。例えば
x(t) = t-1 y(t) = t-1 z(t) = t-1
パラメータ化の定義で、t = 1 はセグメントの開始に対応し、t = 2 は線の終点に対応します。始点と終点に対応する曲線パラメータの範囲はCurve domainと呼ばれます。
理解が必要な他の重要なことは曲線の任意のポイントのパラメータの値は曲線の長さとはなんの関係も無いという事です。先程の直線の例で、t = 0.5 のパラメトリーを考えると、これは(0.5, 0.5, 0.5) となり、すなわちセグメントの真ん中となりますが、別の場合に 0.5 を取ったとき (0.25, 0.25, 0.25) となることもありそれはセグメントの真ん中ではありません。
曲線のすべての可能なパラメータ化の中で、1つ区別されるものがあります。それは natural parametrization(自然パラメトリー化)と言われます。曲線の自然パラメトリー化は性質を持っています: tパラメータのある変化は曲線の長さに同様の変化を与えます。各曲線は1つの自然なパラメトリック化を持っています。
Sverchok同様にBlenderがモデリングにメッシュベースアプローチと取っている為、曲線の視覚化をするためにメッシュに変換する必要があります。通常”Evaluate Curve”ノードか”Curve Length Parameter”ノードで行います。
最後に
なるほど。
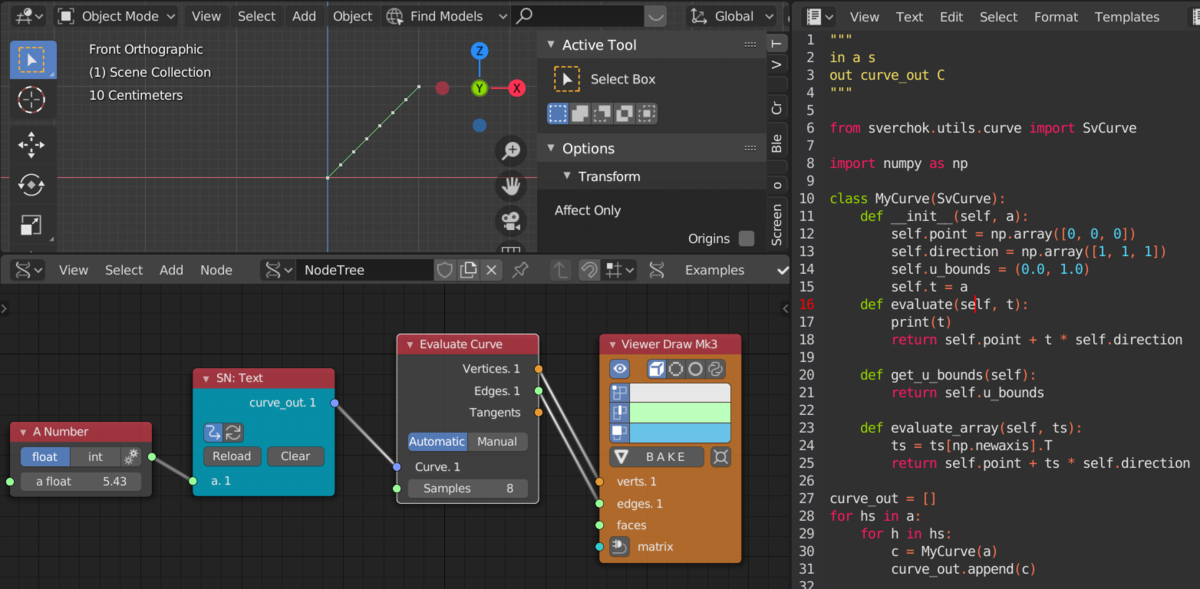
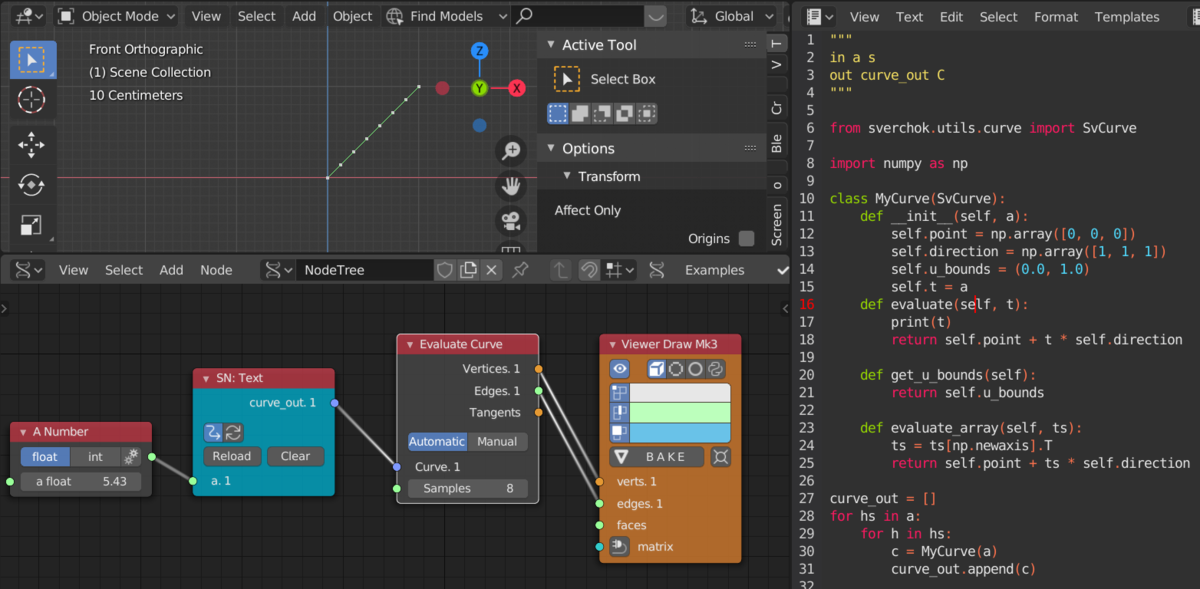
Scriptで描いてみた。線を描くコードは SvLine のそのまま拝借
ここからわかった事。
- curveを出力する場合の出力ソケットは C
- inputは2次元配列に格納されているので for ループを2度行いアンラップする必要がある
- 下記3つの関数は必須
- evaluate はカーブ定義
- get_u_bounds は範囲取得
- evaluate_array は curveを座標にマッピングしたときの座標を定義
"""
in a s
out curve_out C
"""
from sverchok.utils.curve import SvCurve
import numpy as np
class MyCurve(SvCurve):
def __init__(self, a):
self.point = np.array([0, 0, 0])
self.direction = np.array([1, 1, 1])
self.u_bounds = (0.0, 1.0)
self.t = a
def evaluate(self, t):
print(t)
return self.point + t * self.direction
def get_u_bounds(self):
return self.u_bounds
def evaluate_array(self, ts):
ts = ts[np.newaxis].T
return self.point + ts * self.direction
curve_out = []
for hs in a:
for h in hs:
c = MyCurve(a)
curve_out.append(c)