はじめに
Architectureフォルダにある4つのサンプルのうちの1つ。引張カバーというらしい。これはキャンプとかにおいてあるようなものかな?
という事でこの物体の用途はあまりわかってないけど構造を理解する。
全体像
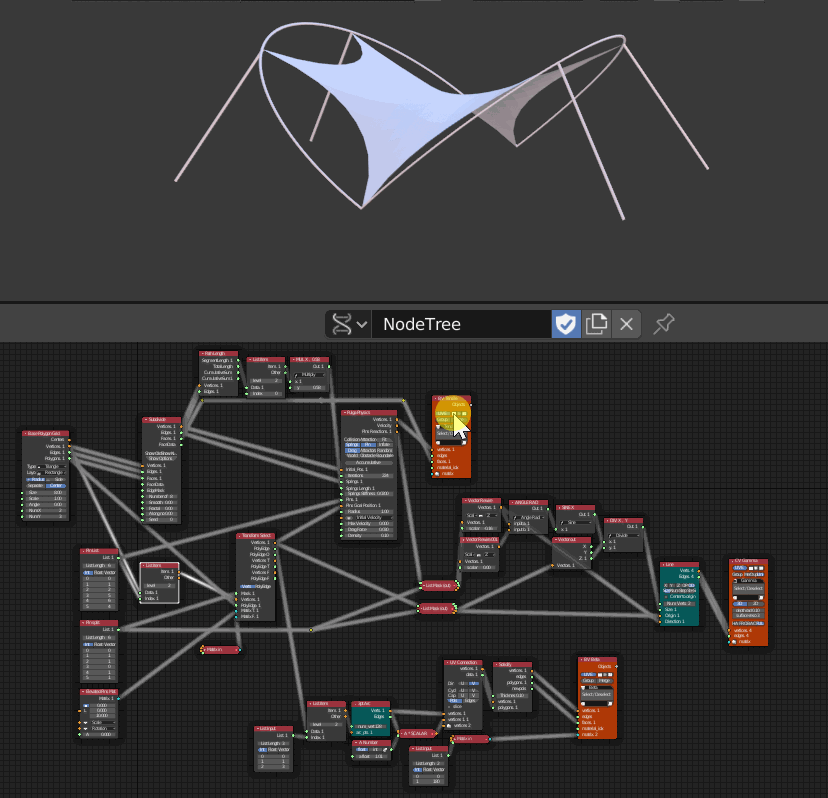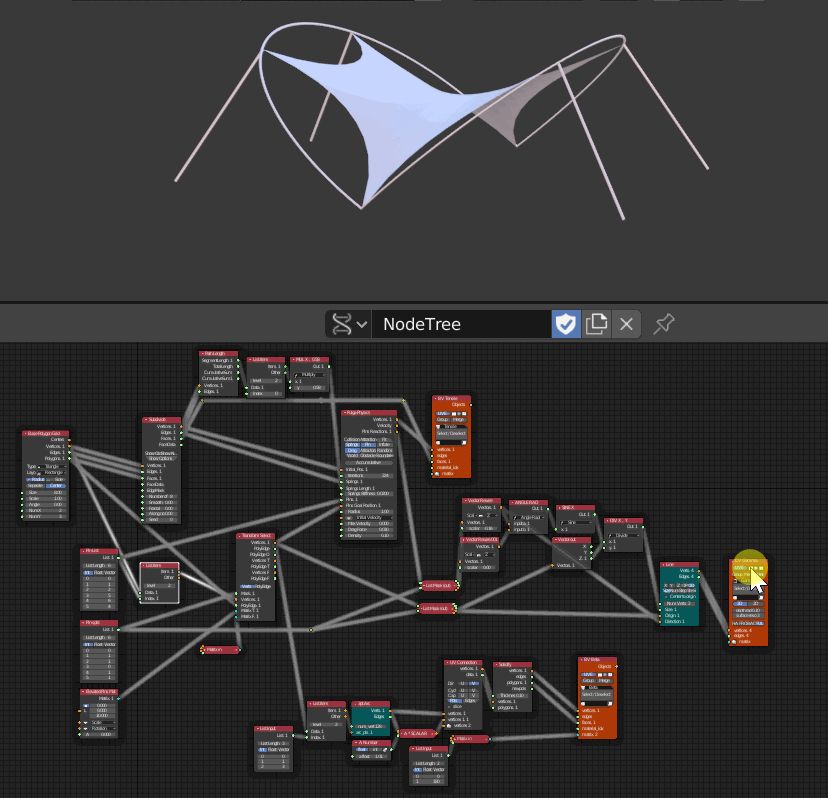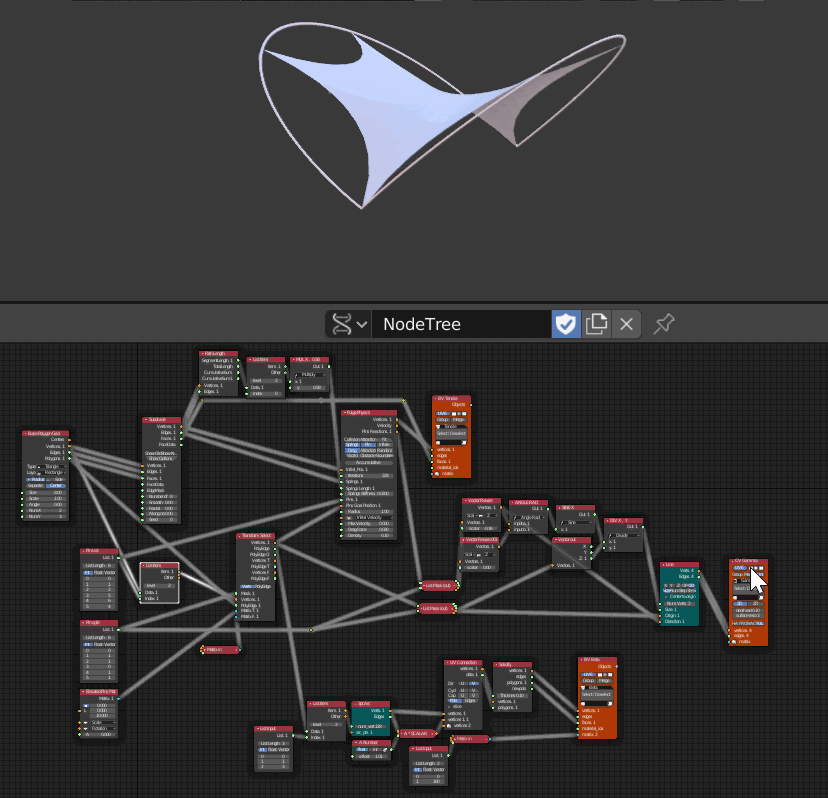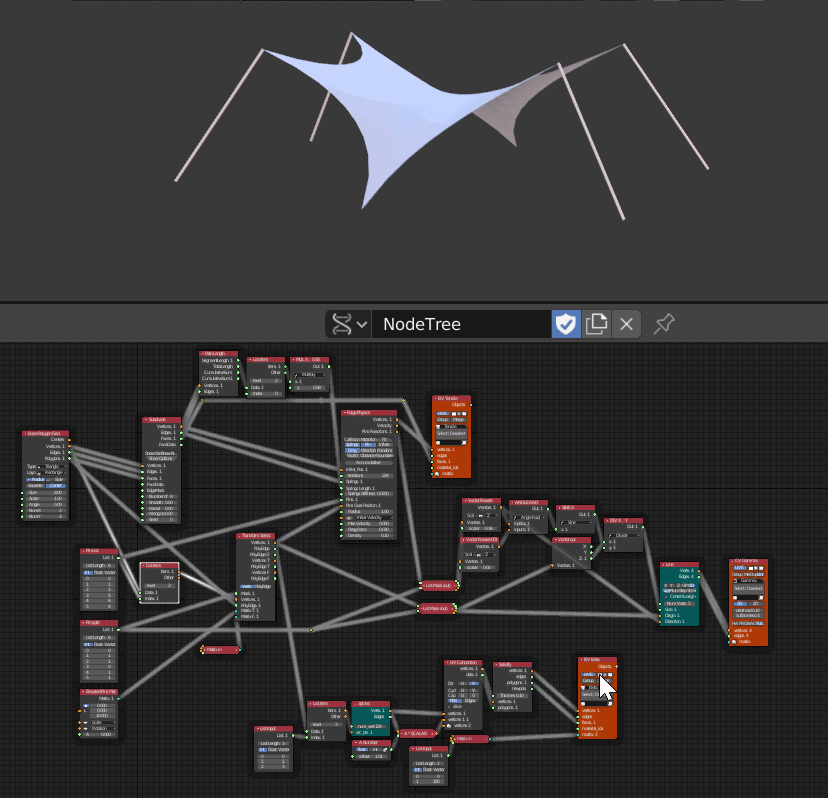
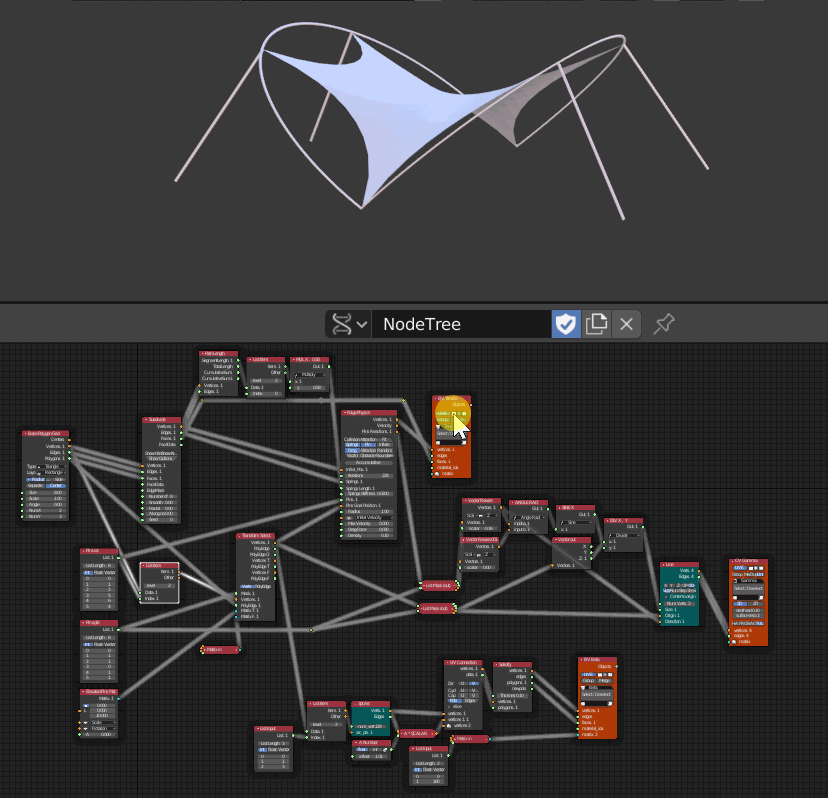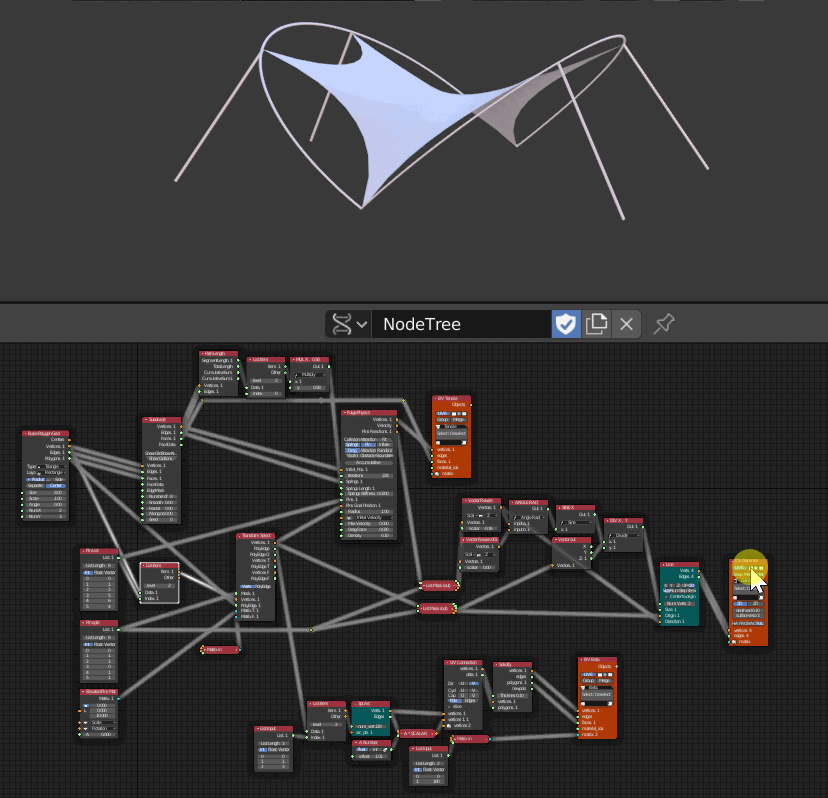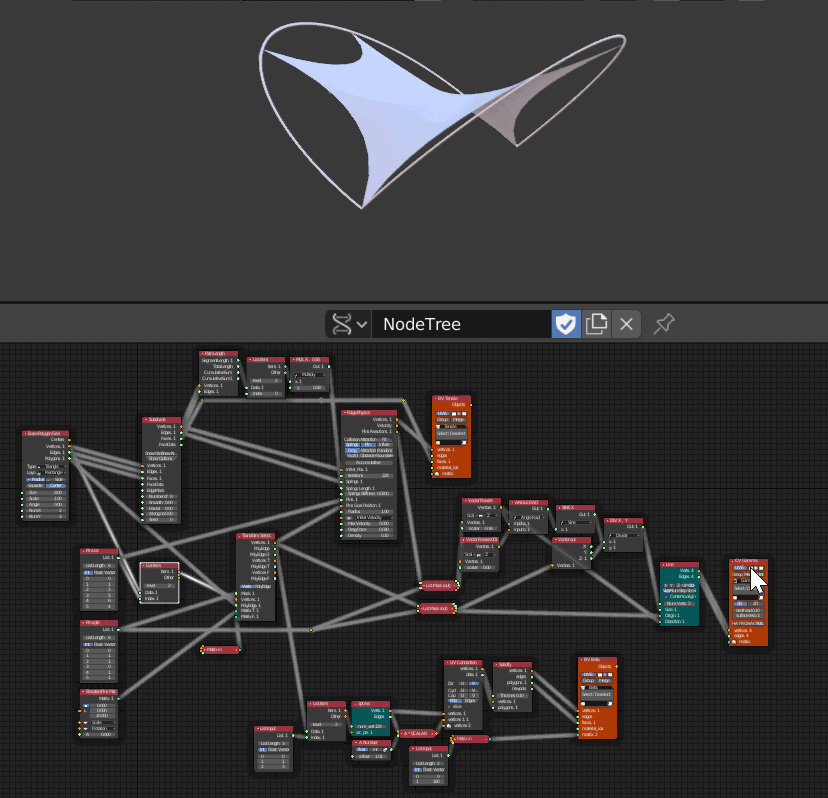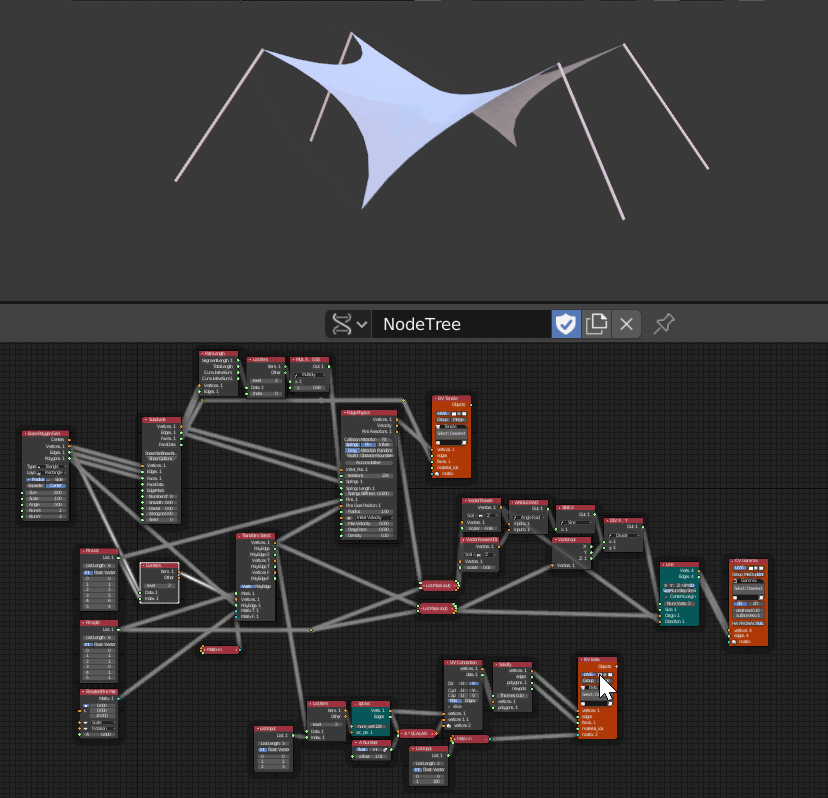
- 3つのViewerが配置されていてそれぞれ順番に非表示にした
- 一番上の Viewerはネットの部分
- 真ん中のViewerは足の部分
- 一番下はネットと足をつなぐフレーム部分
といっても基本的なノードからすべてのViewerに接続されている為、左のノードから順番に見ていくことにする
Base Polygon Grid
- このノードは6角形、3角形または4角形のグリッドを作る。
- ここでは3角形を2x3の6つ配置している。
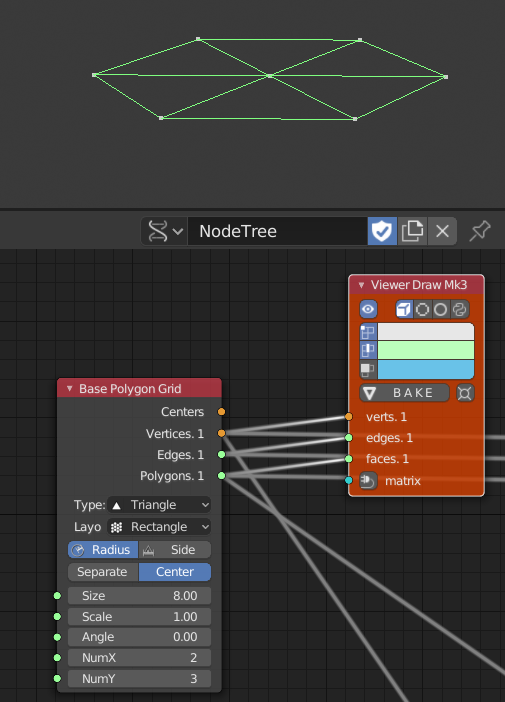
Subdivide
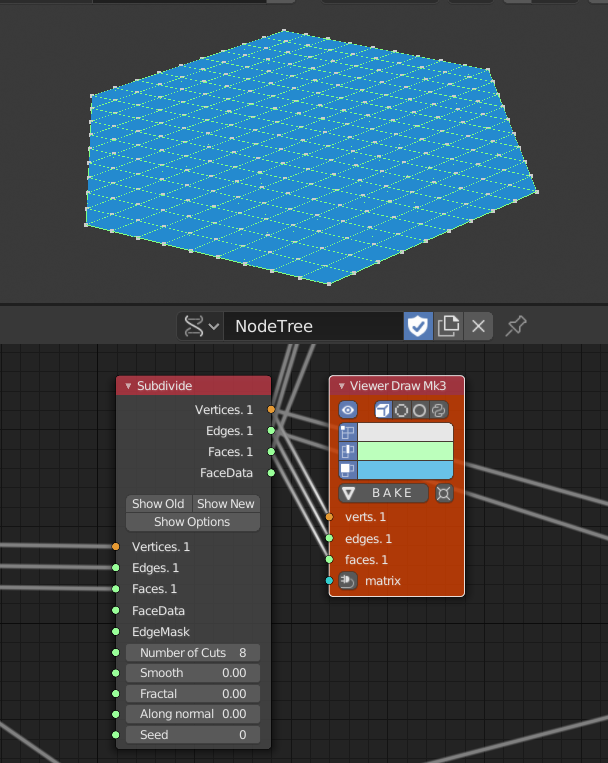
- SubdivideでBase Polygon Gridを細分化している
- これがネットとなる
Pulga Physics
- ノミ物理というノード
- このノードを使えば色々表現出来て、今回のような引っ張られるネットも作れる
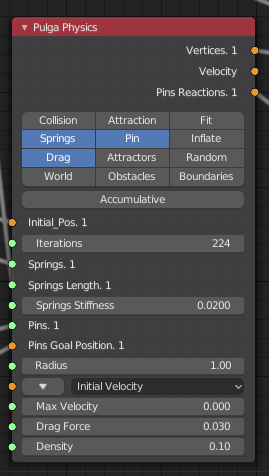
- 上記のノードを見ると有効化されている機能は、Springs(バネ)、Pin、Dragとなる。
- Springs は伸縮性のあるネットを表現する
- Pin は伸縮性のあるネットを固定するポイントを定義
- 今回の例でいうと6つのポイントにネットが引っ張られている
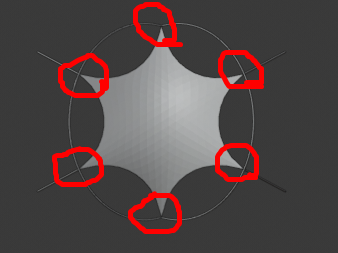
- 今回の例でいうと6つのポイントにネットが引っ張られている
- Drag は抗力でこれを有効にしないとネットは反復回数に応じて上下運動を繰り返す
- Initial_Pos 初期頂点位置
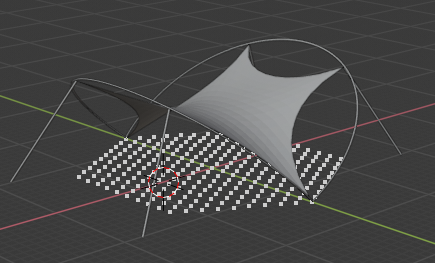
- ネットの下にある白い点が初期位置
- Springs は Subdivide した結果の辺であり伸縮する辺
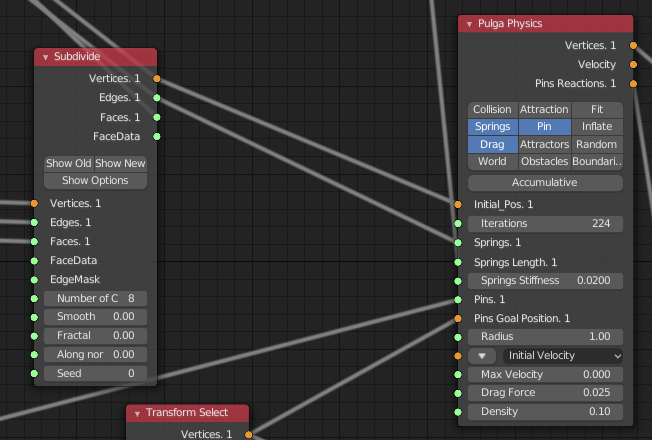
- Springs Length は各辺の長さの 0.58倍
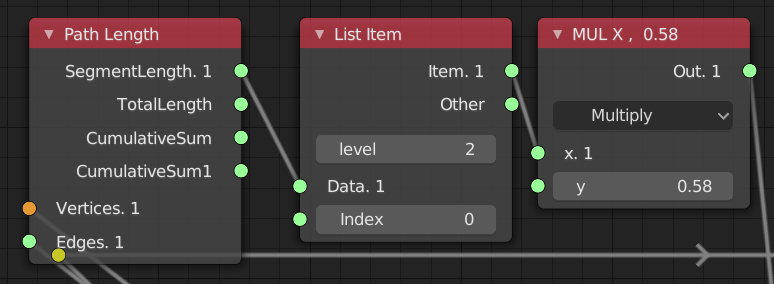
- Path Lengthは各セグメントの長さを取得しリスト化する
- List Item でリスト化されたアイテムの1番目のみを取得
- 何番目をとっても同じ値
- 0.58 を掛けていた結果を Springs Lengthに入力している
- これにより各辺が既に引っ張られた状態になる
- Pin は initial_Posの内、どの頂点を固定するか定めるもので、Pin List(List Item)で定義されている
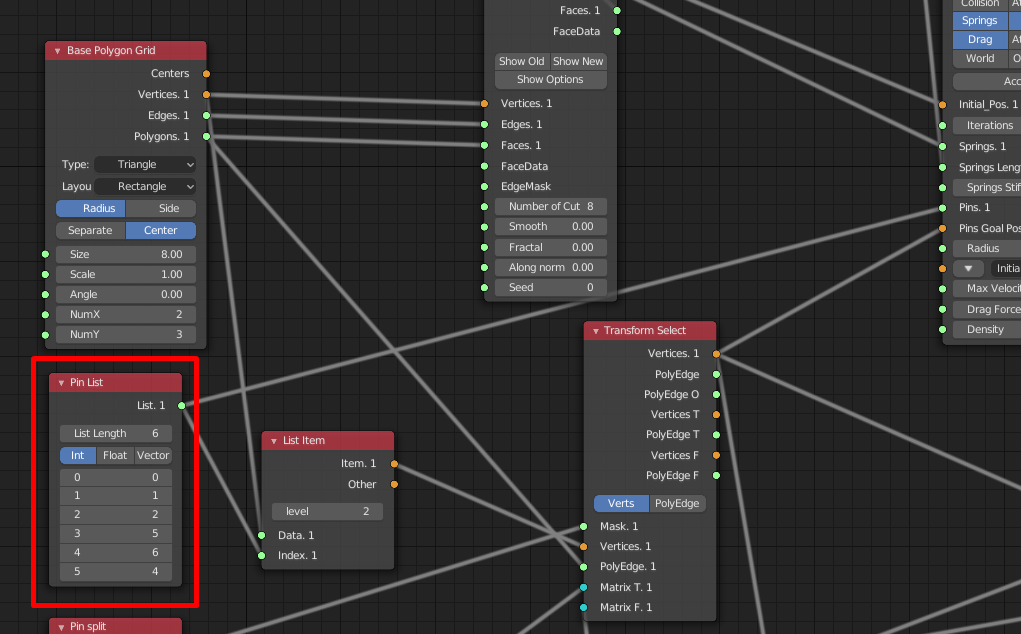
[0, 1, 2, 5, 6, 4]という順番は下記画像の通りBase Polygon Grid の0から順番に頂点のインデックスを時計回りに選択した結果
- Pins Goal Position は固定するピンの座標
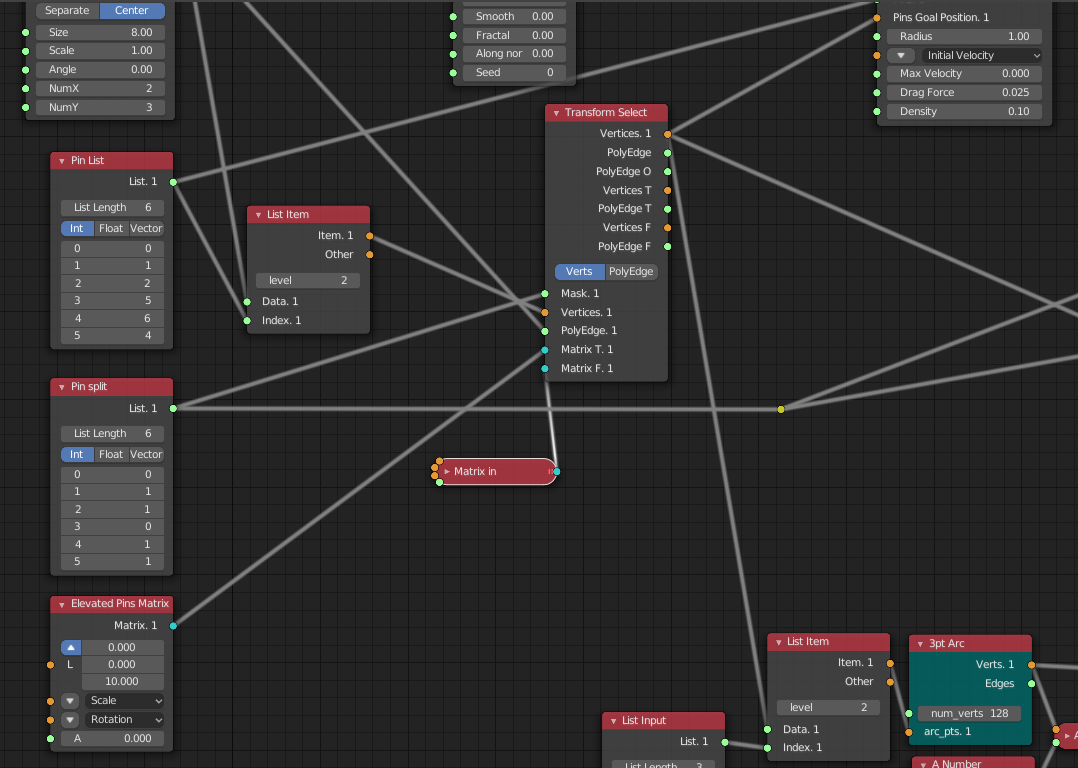
- Pin List の座標をBase Polygon Grid から取得する為 List Item にどちらも接続し、その結果を Transform Select に渡している
- Transform Select では入力された頂点を Mask に応じて変形させる。
- Mask は
[0, 1, 1, 0, 1, 1]となっており[False, True, True, False, True, True]と同義でVertices に入力された6つの頂点の内、2、3、5、6番目の頂点は Matrix T の変形を適用する - Matrix T に接続されているのはZ位置を10にするという移動に関するもの
- Matrix F は1番目と4番目の頂点に適用される変形ですべて0のMatrix が接続されている

- 赤いポイントがPins Goal Positionに入力された頂点の座標
- Mask は
ネットの作成

BMesh Viewer
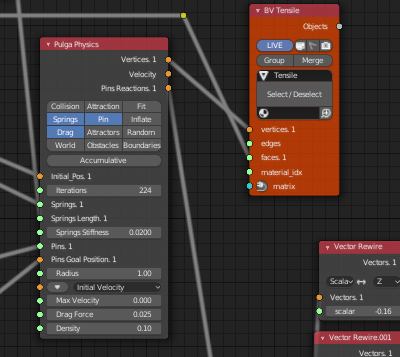
- vertices に接続されているのは Pulga Physics の結果
- Faces に接続されているのは Subdivide した結果の Face
足の作成

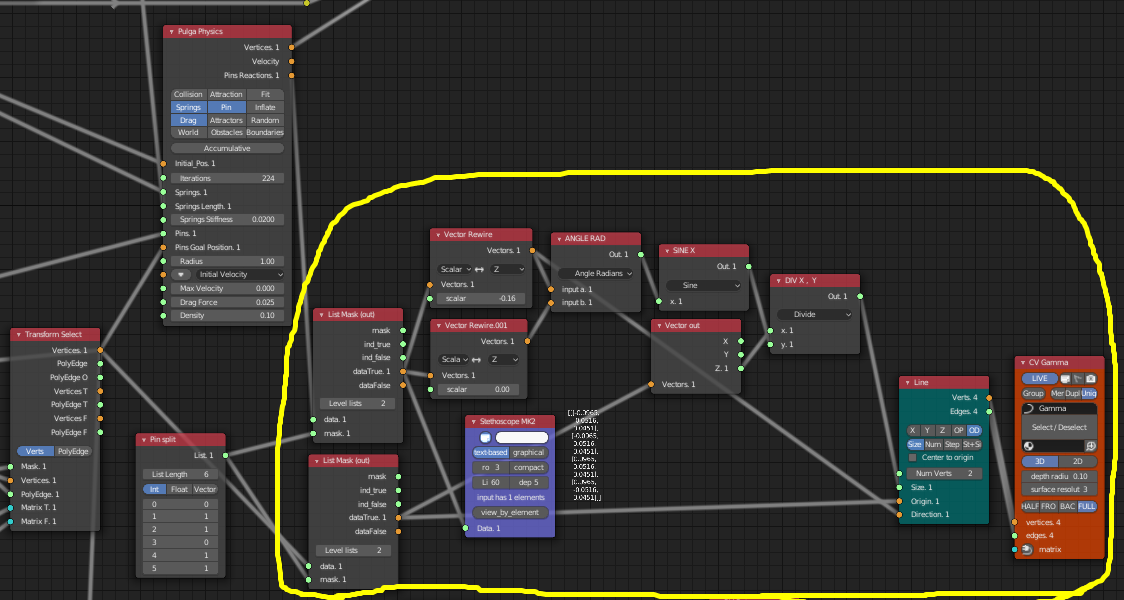
- 元々あったパイプの位置がPulga Physicsによって若干外側にずれる為、ずれた分どのくらいパイプを長くすれば地面に届くか、方向の計算などを行っている
- 上のList Mask(out) はPulga Physicsでシミュレーションした結果の Pinの反応のリストを入力しており、Maskするのは2、3、5、6番目の頂点。
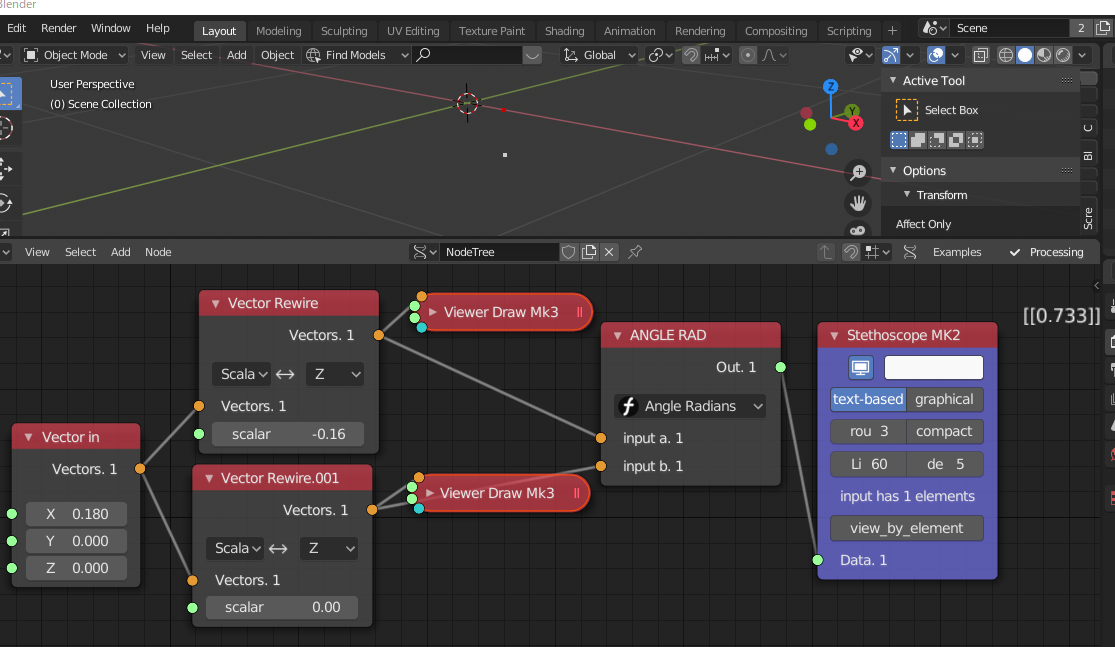
- 2つのVector Rewireで1つはわずかに下にずらしその2つをAngle Radに入力し角度を計算。
- 角度からサインを求めて位置を計算
- 割り算をしてパイプの長さを調整
- ここでは パイプ長/0.9… としているため若干伸びる計算となる
以上
最後に
Vectorから直接角度(RadiansまたはDegree)を求める方法があったなんて。わざわざ分解していたけどそんな必要はなかった模様。