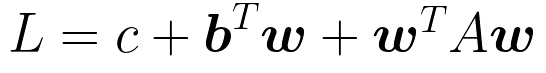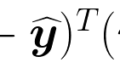はじめに
ディープラーニング勉強中なので今日学んだ式をメモしておきます
評価関数式変形
前回の最終形態
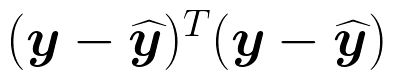
- yハット(予測値)の数式の内訳を見る
- 行列の各行は1件目、2行目が2軒目、…N件目
- 行列の各列は1列目=広さ、2列目=駅からの距離などと考える
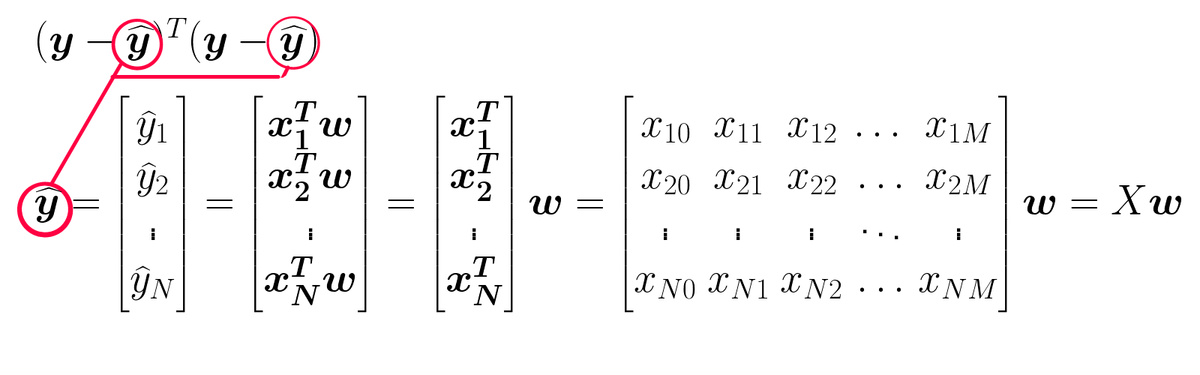
- yハットを上記の式で置き換える
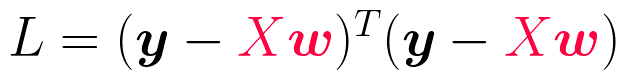
- 転置を括弧内のそれぞれに振り分ける
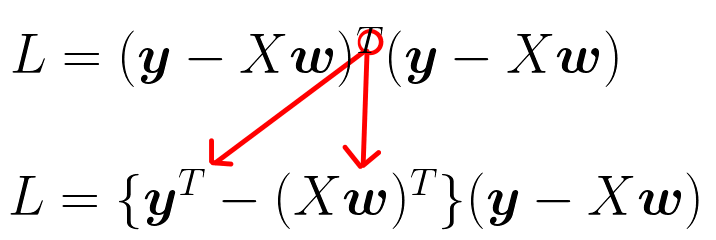
- 転置の公式により変形する
- 🤔先程の振り分け方と違いますが因数分解されたもの内の転置の振り分けと違うという事ですね
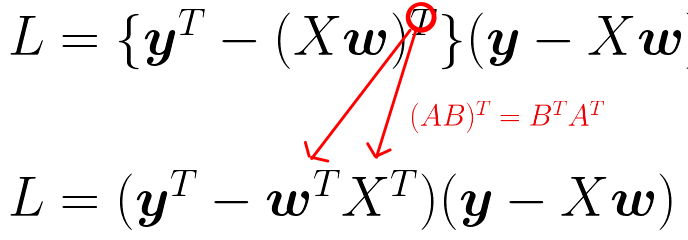
- 展開する
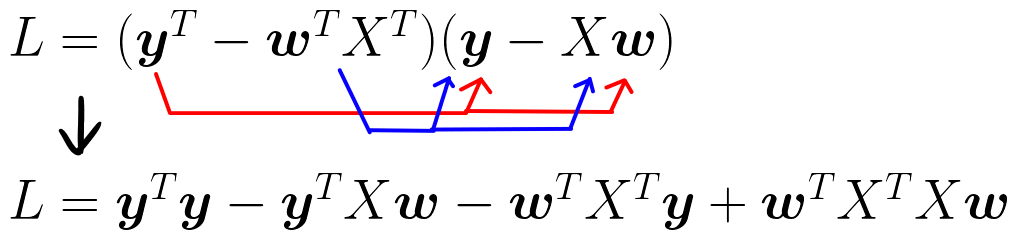
- 転置の公式を使って式変形をして、同じ項をまとめる
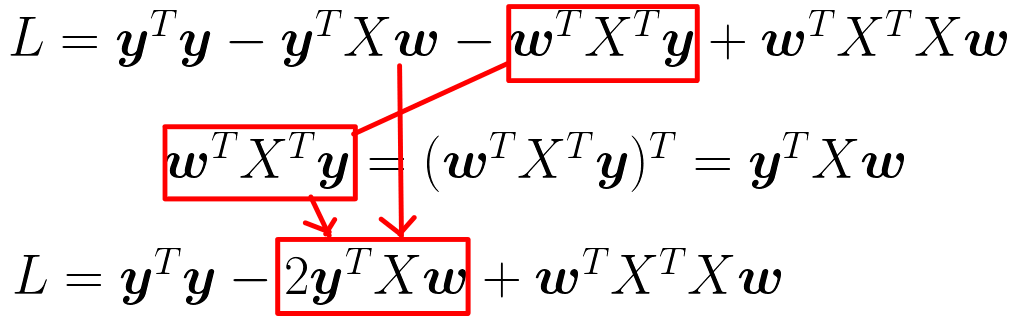
- 重みwについて微分するため、wに関係ないものを別の記号で置き換えていく
- y転置yは実値の為、cに置き換える
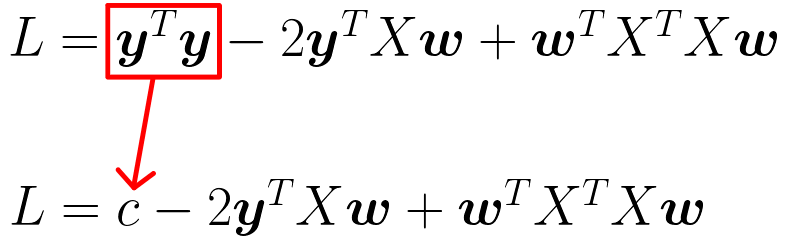
- 赤枠の部分は計算結果がベクトルになるためベクトルの記号に置き換える
- 🤔転置して変形させている部分は今日学んだ範囲では説明がなかった。疑問は忘れずにしておかないといけませんね
- 青枠の部分は計算結果が行列になるため行列の記号で置き換える
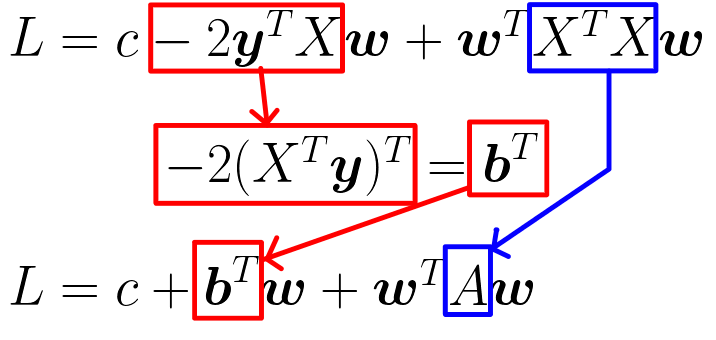
最終結果
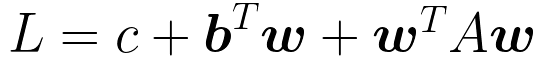
最後に
今の所なんとか食らいついてますが複雑ですね